题目内容
2.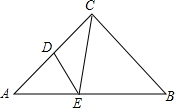 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )| A. | 3$\sqrt{5}$ | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3$\sqrt{5}$+3 |
分析 过点D作D点关于直线AB的对称点D′,连接D′C,交AB于E,连接AD′,首先确定D′C=D′E+EC=DE+CE的值最小,然后根据勾股定理计算.
解答 解:过点D作D点关于直线AB的对称点D′,连接D′C,交AB于E,连接AD′,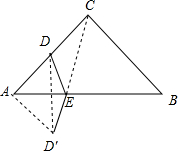
此时DE+CE=D′E+EC=D′C的值最小.
∵在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,
∴∠BAC=45°,DC=3,
由对称性可知∠D′AE=∠DAE=45°,AD′=AD,
∴∠DAD′=90°,
∵D是AC边的中点,AC=6,
∴AD′=3,
根据勾股定理可得:D′C=$\sqrt{A{C}^{2}+AD{′}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴△CDE周长的最小值:DE+CE+DC=D′C+DC=3$\sqrt{5}$+3
故选D.
点评 此题考查了轴对称求最短路线的问题,确定动点E何位置时,使EC+ED的值最小是关键.

练习册系列答案
相关题目
14.下列图形中即是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
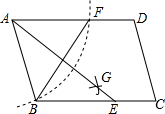 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为16.
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为16. 如图,在△ABC中,D是BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知BE=3cm,BC=6cm,则△BDE的周长为9cm.
如图,在△ABC中,D是BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知BE=3cm,BC=6cm,则△BDE的周长为9cm.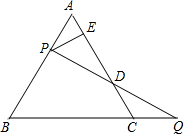 如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论:
如图,等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上的一点,当PA=CQ时,连接PQ交AC于点D,下列结论: 如图,在正方形ABCD中,E是CD上一点,F是CB延长线上一点,且DE=BF,AF,AE之间有怎样的关系?请说明理由.
如图,在正方形ABCD中,E是CD上一点,F是CB延长线上一点,且DE=BF,AF,AE之间有怎样的关系?请说明理由.