题目内容
7．
如图：在△ABC中，∠BAC=90°，AD⊥BC于点D，点E是AD上一点，求证：∠BED＞∠C．
分析 根据直角三角形的性质得到∠BAD=∠C，根据三角形的外角的性质得到∠BED＞∠BAD，等量代换得到答案．
解答 证明：∵∠BAC=90°，
∴∠BAD+∠DAC=90°，
∵AD⊥BC，
∴∠C+∠DAC=90°，
∴∠BAD=∠C，
∵∠BED＞∠BAD，
∴∠BED＞∠C．
点评 本题考查的是三角形的外角的性质、直角三角形的性质，掌握三角形的一个外角大于和它不相邻的任何一个内角是解题的关键．
练习册系列答案
相关题目
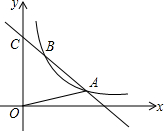如图：一次函数的图象与y轴交于C（0，4），且与反比例函数y=$\frac{k}{x}$（x＞0）的图象在第一象限内交于A（3．a），B（1，b）两点．
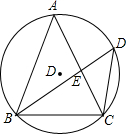如图，AB=AC，弦BD⊥AC于点E．
如图，在△ABC中，∠ABC=90°，CD⊥AB于点D，若AB=16，BC=12，求sinα．