题目内容
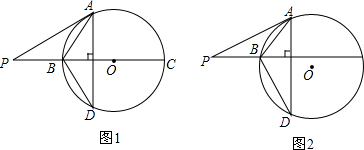
2. 如图,AB=AC,弦BD⊥AC于点E.
如图,AB=AC,弦BD⊥AC于点E.(1)求证:BD-CD=2ED;
(2)若BD=11,CD=5,求AB的长.
分析 (1)在EB上截取EF=ED,如图,则CE垂直平分DF,根据等腰三角形的判定与性质得CD=CF,∠1=∠2,加上∠2+∠3=∠4+∠5,∠1=∠5,易得∠3=∠4,所以FB=FC,则FB=CD,而BD-BF=DF=2ED,所以BD-CD=2ED;
(2)由(1)的结论可计算出ED=3,在Rt△CDE中,利用勾股定理计算出CE=4,设AB=x,则AC=x,AE=x-4,然后在Rt△ABE中,利用勾股定理得到82+(x-4)2=x2,然后解方程求出x即可.
解答 (1)证明:在EB上截取EF=ED,如图,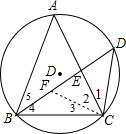
∵BD⊥AC,
∴CE垂直平分DF,
∴CD=CF,∠1=∠2,
∵AB=AC,
∴∠ABC=∠ACB,即∠2+∠3=∠4+∠5,
而∠1=∠5,
∴∠3=∠4,
∴FB=FC,
∴FB=CD,
∴BD-BF=DF=2ED,
即BD-CD=2ED;
(2)解:∵BD=11,CD=5,
∴2ED=11-5,解得ED=3,
在Rt△CDE中,CE=$\sqrt{{5}^{2}-{3}^{2}}$=4,
设AB=x,则AC=x,
∴AE=x-4,
而BE=BD-DE=11-3=8,
在Rt△ABE中,82+(x-4)2=x2,解得x=10,
即AB的长为10.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了勾股定理.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
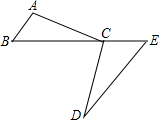 已知:如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:∠A=∠DCE.
已知:如图,C为BE上一点,点A,D分别在BE两侧.AB∥ED,AB=CE,BC=ED.求证:∠A=∠DCE. 开学初,某校组织开展了“创建温馨教室”活动,一中队的班干部在布置教室时需要一些星形图片,他们先把正方形纸片剪去四个面积相等的扇形,然后将所得图形(如图中去掉阴影后的剩余部分)涂上不同颜色而得到星形图片.
开学初,某校组织开展了“创建温馨教室”活动,一中队的班干部在布置教室时需要一些星形图片,他们先把正方形纸片剪去四个面积相等的扇形,然后将所得图形(如图中去掉阴影后的剩余部分)涂上不同颜色而得到星形图片. 如图:在△ABC中,∠BAC=90°,AD⊥BC于点D,点E是AD上一点,
如图:在△ABC中,∠BAC=90°,AD⊥BC于点D,点E是AD上一点, 把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个.
把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个.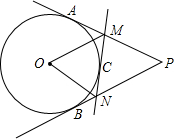 如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )
如图所示,已知PA、PB切⊙O于A、B两点,C是$\widehat{AB}$上一动点,过C作⊙O的切线交PA于点M,交PB于点N,已知∠P=56°,则∠MON=( )