题目内容
6.学校财务老师到体育用品商店购买篮球和足球,已知购买1个篮球和1个足球共需210元,财务老师一共用550元购买了3个同样的篮球和2个同样的足球.(1)求购买每个篮球和每个足球各是多少元?
(2)如果学校用1000元现金去购买篮球和足球,能否各购买5个?为什么?
(3)如果学校计划用不多于1000元的现金去购买篮球和足球共10个,求篮球最多能购买多少个?
分析 (1)设每个篮球的售价是x元,每个足球的售价是y元,根据题意列出方程组,求出方程组的解即可;
(2)求出篮球和足球各购买5个的钱数,相加后与1000元比较大小即可求解;
(3)设篮球购买a个,则足球购买(10-a)个,根据题意列出不等式,求出不等式的解集即可确定出最多购买的篮球.
解答 解:(1)设每个篮球的售价是x元,每个足球的售价是y元,依题意有
$\left\{\begin{array}{l}{x+y=210}\\{3x+2y=550}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=130}\\{y=80}\end{array}\right.$.
答:每个篮球的售价是130元,每个足球的售价是80元;
(2)130×5+80×5
=650+400
=1050(元),
∵1050元>1000元,
∴不能各购买5个;
(3)设篮球购买a个,则足球购买(10-a)个,依题意有
130a+80(10-a)≤1000,
解得a≤4.
故篮球最多能购买4个.
点评 此题考查了一元一次不等式的应用,以及二元一次方程组的应用,弄清题中的等量关系及不等关系是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列分解因式中,结果正确的是( )
| A. | x2-1=(x-1)2 | B. | x2+2x-1=(x+1)2 | C. | x2-6x+9=x(x-6)+9 | D. | 2x2-2=2(x+1)(x-1) |
11.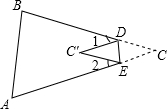 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
 如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )
如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )| A. | 33° | B. | 34° | C. | 31° | D. | 32° |
 在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求
在矩形纸片ABCD中,AD=4cm,AB=10cm,按图所示方式折叠,使点B与点D重合,折痕为EF,求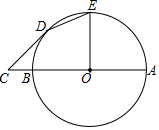 已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2
已知AB为⊙O的直径,C为AB延长线上一点,CD切⊙O于点D,CD=4,BC=2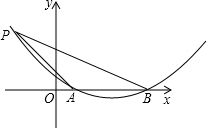 如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求:
如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,AB=4,P是抛物线上一点,它的横坐标为-2,∠PAO=45°,cot∠PBO=$\frac{7}{3}$,求: 如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( )
如图所示,在?ABCD中,对角线AC,BC相交于点O,已知△BOC与△AOB的周长之差为4,?ABCD的周长为28,则BC的长度为( ) 如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大.
如图,长方形硬纸板以其中任意一边为轴旋转都可得到一个圆柱,你认为以3厘米长的边为轴旋转得到的圆柱体积较大. 若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.
若将三个数$\sqrt{3}$,3$\sqrt{2}$,2$\sqrt{3}$表示在数轴上,则能被如图所示的墨迹覆盖的数是$\sqrt{3}$.