题目内容
16.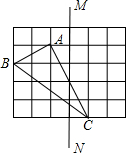 如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题.
如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题.(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)△AB1C的面积为7;
(3)试判断△ABC的形状并说明理由.
分析 (1)根据网格结构找出点A、B、C关于直线MN的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据三角形的面积等于三角形所在的矩形面积减去四周三个直角三角形的面积列式计算即可得解;
(3)利用勾股定理列式求出AB、BC、AC,再根据勾股定理逆定理解答.
解答 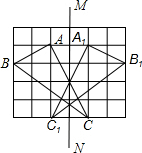 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;
(2)△AB1C的面积=4×4-$\frac{1}{2}$×1×4-$\frac{1}{2}$×2×3-$\frac{1}{2}$×2×4
=16-2-3-4
=16-9
=7.
故答案为:7;
(3)由勾股定理得,AB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
AC=$\sqrt{{2}^{2}+{4}^{2}}$=$\sqrt{20}$,
∵AB2+AC2=($\sqrt{5}$)2+($\sqrt{20}$)2=25,
BC2=52=25,
∴AB2+AC2=BC2,
∴△ABC是直角三角形.
点评 本题考查了利用轴对称变换作图,勾股定理,勾股定理逆定理,三角形的面积,熟练掌握网格结构并准确找出对应点的位置是解题的关键.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
6.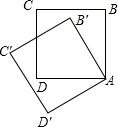 如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
 如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )
如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
4.已知∠A=60°,则∠A的补角是( )
| A. | 160° | B. | 120° | C. | 60° | D. | 30° |
11. 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )
 如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )
如图,将两根钢条AB、CD的中点O连在一起,使AB、CD可以绕点O自由转动,就做成一个测量工件,则AC的长等于内槽宽BD,则判定△OBD≌△OAC的理由是( )| A. | 边边边 | B. | 角边角 | C. | 边角边 | D. | 角角边 |
1.如果多项式x2-mx+16是一个完全平方式,则m的值是( )
| A. | 4 | B. | ±4 | C. | 8 | D. | ±8 |
 直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=89°,则∠2=44°.
直线l1∥l2,一块含45°角的直角三角板如图放置,∠1=89°,则∠2=44°.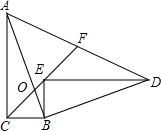 如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.