题目内容
12.当x是多少时,$\frac{\sqrt{x}}{2x-1}$在实数范围内有意义.分析 根据被开方数大于等于0,分母不等于0列式计算即可得解.
解答 解:依题意有x≥0且2x-1≠0,
解得x≥0且x≠$\frac{1}{2}$.
故当x≥0且x≠$\frac{1}{2}$时,$\frac{\sqrt{x}}{2x-1}$在实数范围内有意义.
点评 本题考查了二次根式有意义的条件,主要利用了二次根式有意义,被开方数大于等于0,分式有意义,分母不等于0.

练习册系列答案
相关题目
9. 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
请根据图表信息解答下列问题:
(1)本次共抽样调查120个学生;
(2)填空:频数分布表中的m=30,n=0.3;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查,调查的项目有:公共汽车、小车、摩托车、自行车、其它(每位同学仅选一项).根据调查结果绘制了如下不完整的频数分布表和扇形统计图:| 交通方式 | 频数(人数) | 频率 |
| 公共汽车 | m | 0.25 |
| 小车 | 24 | 0.20 |
| 摩托车 | 36 | n |
| 自行车 | 18 | 0.15 |
| 其它 | 12 | 0.10 |
(1)本次共抽样调查120个学生;
(2)填空:频数分布表中的m=30,n=0.3;
(3)在扇形统计图中,请计算出“摩托车”所在的扇形的圆心角的度数.
7.计算3a3b2÷a2+(a3b-3ab3-5a2b)÷b的结果为( )
| A. | a3+6ab2-5a2 | B. | a3-6ab2-5a2 | C. | a3-5a2 | D. | a2+6ab-5a |
1.已知x+y=7,xy=-8,下列各式计算结果不正确的是( )
| A. | (x-y)2=81 | B. | x2+y2=65 | C. | x2+y2-xy=71 | D. | x2-y2=±63 |
2.下列各式中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{2\frac{1}{4}}$=1$\frac{1}{2}$ | C. | $\sqrt{(-3)^{2}}$=-3 | D. | $\root{3}{-27}$=-9 |
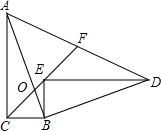 如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
如图,在Rt△ABC中,∠ACB=90°,sin∠CAB=$\frac{1}{3}$,点O在AB上,且CB=CO=3,若Rt△ABC绕点B顺时针旋转一定角度后得到Rt△BED,且E落在CO的延长线上,连接AD交CO的延长线于F,则AF的长为7.
 已知,在Rt△ABC中,∠ACB=90°,请利用直角三角形全等的HL判定定理,求作Rt△DEF,使Rt△DEF≌Rt△ABC.
已知,在Rt△ABC中,∠ACB=90°,请利用直角三角形全等的HL判定定理,求作Rt△DEF,使Rt△DEF≌Rt△ABC.