题目内容
 如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,每个小方格都是边长为1个单位的小正方形,A、B、C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF∽△ABC,且相似比为2:1;
(2)求∠D的正弦值;
(3)若△ABC外接圆的圆心为P,则点P的坐标为
考点:作图—相似变换,三角形的外接圆与外心
专题:
分析:(1)根据网格结构,作出DE=2AB,EF=2BC,DF=2AC的三角形即可;
(2)作FG⊥DE于G,在Rt△DFG中利用正弦函数的定义即可求解;
(3)设点P的坐标为(x,y),根据“三角形外接圆的圆心到三角形三个顶点的距离相等”列出等式,化简即可得出点P的坐标.
(2)作FG⊥DE于G,在Rt△DFG中利用正弦函数的定义即可求解;
(3)设点P的坐标为(x,y),根据“三角形外接圆的圆心到三角形三个顶点的距离相等”列出等式,化简即可得出点P的坐标.
解答:解:(1)如下图所示,△DEF即为所求;
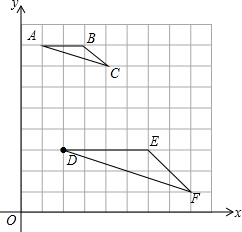
(2)如图,作FG⊥DE于G,
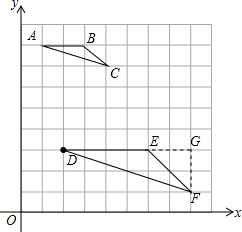
∵在Rt△DFG中,FG=2,DG=6,
∴DF=
=
=2
,
∴sin∠D=
=
=
;
(3)设点P的坐标为(x,y);
∵△ABC外接圆的圆心为P,
∴PA=PB=PC,
∵A(1,8),B(3,8),C(4,7),
∴(1-x)2+(8-y)2=(3-x)2+(8-y)2=(4-x)2+(7-y)2,
化简后得x=2,y=6,
因此点P的坐标为(2,6).
故答案为(2,6).

(2)如图,作FG⊥DE于G,

∵在Rt△DFG中,FG=2,DG=6,
∴DF=
| FG2+DG2 |
| 22+62 |
| 10 |
∴sin∠D=
| FG |
| DF |
| 2 | ||
2
|
| ||
| 10 |
(3)设点P的坐标为(x,y);
∵△ABC外接圆的圆心为P,
∴PA=PB=PC,
∵A(1,8),B(3,8),C(4,7),
∴(1-x)2+(8-y)2=(3-x)2+(8-y)2=(4-x)2+(7-y)2,
化简后得x=2,y=6,
因此点P的坐标为(2,6).
故答案为(2,6).
点评:本题考查了作图-相似变换,锐角三角函数的定义,勾股定理,三角形的外接圆与外心,两点间的距离公式,难度适中.

练习册系列答案
相关题目
青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米,将2500000用科学记数法表示为( )
| A、2.5×106 |
| B、2.5×107 |
| C、0.25×107 |
| D、25×105 |
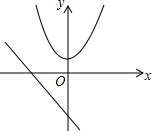 如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.
如图,坐标系中有抛物线c:y=x2+m和直线l:y=-2x-2.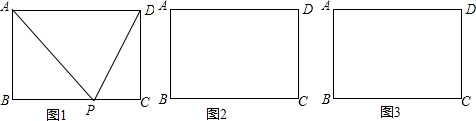
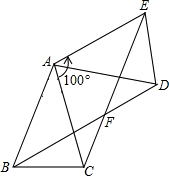 如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
如图,在△ABC中,已知AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD,CE交于点F.
 用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x米,窗户的透光面积为S平方米,则S关于x的函数关系式为
用长为8米的铝合金制成如图所示的窗框,若设窗框的宽为x米,窗户的透光面积为S平方米,则S关于x的函数关系式为