题目内容
13.已知分式($\frac{x}{x+1}+\frac{1}{x-1}$)$÷\frac{1}{{x}^{2}-1}$,及一组数据:-2,-1,1,2,0.(1)从已知数据中随机选取一个数代替x,能使已知分式有意义的概率是多少?
(2)先将已知分式化简,再从已知数据中选取一个你喜欢的,且使已知分式有意义的数代替x求值.
分析 (1)根据分式有意义的条件及概率公式即可得出结论;
(2)先根据分式混合运算的法则把原式进行化简,由分式有意义的条件选出合适的x的值代入进行计算即可.
解答 解:(1)∵分式有意义,
∴x2-1≠0,即x≠±1,
∴使已知分式有意义的概率=$\frac{3}{5}$;
(2)原式=$\frac{x(x-1)+x+1}{(x+1)(x-1)}$•(x+1)(x-1)
=x2-x+x+1
=x2+1,
当x=0时,原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.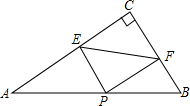 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )| A. | 5 | B. | $\frac{3}{2}$ | C. | 4 | D. | $\frac{24}{5}$ |
 如图,反比例函数y=$\frac{6}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是(1)、(2)、(4)(将正确的结论填在横线上).
如图,反比例函数y=$\frac{6}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是(1)、(2)、(4)(将正确的结论填在横线上).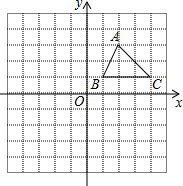 如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.
如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.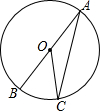 如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=20°.
如图,在⊙O中,AB是直径,C是圆上一点,且∠BOC=40°,则∠ACO=20°. 画图并填空:
画图并填空: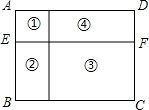 如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.
如图,要用60m的篱笆在一块足够大的空地上围出四个花园,已知①号花园为正方形,且④号花园的周长等于①号和②号花园周长之和.设CD的长为xm,②号花园的面积为ym2.