题目内容
5．某电器商场销售A、B两种型号计算器，两种计算器的进货价格分别为每台30元，40元，商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．求商场销售A、B两种型号计算器的销售价格分别是多少元？（利润=销售价格-进货价格）分析 首先设A种型号计算器的销售价格是x元，A种型号计算器的销售价格是y元，根据题意可等量关系：①5台A型号和1台B型号计算器，可获利润76元；②销售6台A型号和3台B型号计算器，可获利润120元，根据等量关系列出方程组，再解即可．
解答 解：（1）设A种型号计算器的销售价格是x元，B种型号计算器的销售价格是y元，由题意得：
$\left\{\begin{array}{l}{5（x-30）+（y-40）=76}\\{6（x-30）+3（y-40）=120}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=42}\\{y=56}\end{array}\right.$，
答：A种型号计算器的销售价格是42元，B种型号计算器的销售价格是56元．
点评 此题主要考查了二元一次方程组的应用，解题关键是弄清题意，合适的等量关系，列出方程组．
练习册系列答案
阅读快车系列答案
相关题目
15．
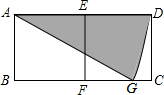如图，两个小正方形的边长都是1，以A为圆心，AD为半径作弧交BC于点G，则图中阴影部分的面积为（ ）
如图，两个小正方形的边长都是1，以A为圆心，AD为半径作弧交BC于点G，则图中阴影部分的面积为（ ）| A． | $\frac{π}{3}$ | B． | $\frac{2π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{2}$ |
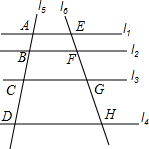如图，四条平行直线l1，l2，l3，l4被直线l5，l6所截，AB：BC：CD=1：2：3，若FG=3，则线段EF和线段GH的长度之和是（ ）
如图，在△ABC中，∠A=40°，∠B=72°，CD是AB边上的高，CE是∠ACB的平分线，DF⊥CE于F，求∠CDF的度数．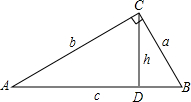
小叶从计算中得到这样的结论：如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．设BC=a，AC=b，AB=c，CD=h，则有等式$\frac{1}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=$\frac{1}{{h}^{2}}$成立．请你判断小叶的结论是否正确？若正确，请给予证明；若不正确，请说明理由．