题目内容
2.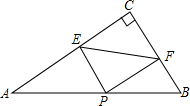 如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )
如图,在△ABC中,AB=10,BC=6,AC=8,PE⊥AC于E,PF⊥BC于F.则线段EF长的最小值为( )| A. | 5 | B. | $\frac{3}{2}$ | C. | 4 | D. | $\frac{24}{5}$ |
分析 先由矩形的判定定理推知四边形PECF是矩形;连接PC,则PC=EF,所以要使EF,即PC最短,只需PC⊥AB即可;然后根据三角形的等积转换即可求得PC的值.
解答 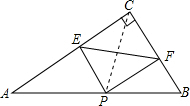 解:连接PC.
解:连接PC.
∵PE⊥AC,PF⊥BC,
∴∠PEC=∠PFC=90°,
又∵AB=10,BC=6,AC=8,
∴AB2=AC2+BC2,
∴∠ACB=90°,
∴四边形ECFP是矩形,
∴EF=PC,
∴当PC最小时,EF也最小,即当CP⊥AB时,PC最小,
∵AC=8,BC=6,
∴AB=10,
∴$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•PC,
∴PC=$\frac{24}{5}$,即线段EF长的最小值为$\frac{24}{5}$.
故选:D.
点评 本题考查了勾股定理、矩形的判定与性质、垂线段最短.利用“两点之间垂线段最短”找出PC⊥AB时,PC取最小值是解答此题的关键.

练习册系列答案
相关题目
11.先化简,再求值:$\frac{12-3x}{x-2}$÷(x+2-$\frac{12}{x-2}$)•$\frac{{x}^{2}+8x+16}{3}$,其中x=3tan30°-8cos60°.
12. 如图,直线a、b被直线c所截,给出的下列条件中不能得出结论a∥b的是( )
如图,直线a、b被直线c所截,给出的下列条件中不能得出结论a∥b的是( )
 如图,直线a、b被直线c所截,给出的下列条件中不能得出结论a∥b的是( )
如图,直线a、b被直线c所截,给出的下列条件中不能得出结论a∥b的是( )| A. | ∠1=∠3 | B. | ∠1=∠4 | C. | ∠1=∠2 | D. | ∠1+∠2=180° |
 如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.
如图,已知等腰△ABC中,AB=AC,AD⊥BC,CE⊥AB,垂足分别为D、E.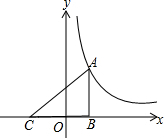 如图,点A是反比例函数y=$\frac{k}{x}$(x>0)图象上一点,AB⊥x轴于点B,点C在x轴上,且OB=OC,若△ABC的面积等于6,则k的值等于( )
如图,点A是反比例函数y=$\frac{k}{x}$(x>0)图象上一点,AB⊥x轴于点B,点C在x轴上,且OB=OC,若△ABC的面积等于6,则k的值等于( )