题目内容
4. (1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$
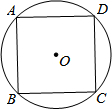
(1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$(2)如图,四边形ABCD是⊙O的内接正方形,若正方形的面积等于4,求⊙O的面积.
分析 (1)分别求出两个不等式的解集,再取它们的公共部分即可;
(2)根据正方形的面积公式求得半径,然后根据圆的面积公式求解即可.
解答 解:(1)$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$
由x≤3x+2得:x≥-1,
由x-1<2-2x得:x<1,
故原不等式的解集为:-1≤x<1;
(2)∵正方形的面积等于4,
∴正方形的边长AB=2,
则半径是2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,
∴⊙O的面积=π($\sqrt{2}$)2=2π.
故答案是:2π.
点评 本题考查了一元一次不等式组的解法、正多边形的计算、正方形的性质;根据正方形的面积求得半径是解决问题(2)的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.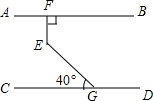 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
 如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )
如图,AB∥CD,EF⊥AB于F,∠EGC=40°,则∠FEG=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
15.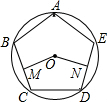 如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
 如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )
如图,正五边形ABCDE内接于⊙O,点M为BC中点,点N为DE中点,则∠MON的大小为( )| A. | 108° | B. | 144° | C. | 150° | D. | 166° |
12.下列叙述正确的是( )
| A. | 方差越大,说明数据就越稳定 | |
| B. | 有一个锐角相等的两个直角三角形相似 | |
| C. | 在不等式两边同乘以或同除以一个不为0的数时,不等号的方向不变 | |
| D. | 两边及其一边的对角对应相等的两个三角形全等 |

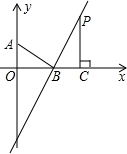 如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别为(0,3),(4,0),过点B作直线l⊥AB,P是直线l上一动点,作PC⊥x轴,垂足为C,设点P的横坐标为a,若a>4,求BP的长.(用含a的代数式表示)
如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别为(0,3),(4,0),过点B作直线l⊥AB,P是直线l上一动点,作PC⊥x轴,垂足为C,设点P的横坐标为a,若a>4,求BP的长.(用含a的代数式表示)