题目内容
9.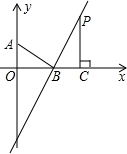 如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别为(0,3),(4,0),过点B作直线l⊥AB,P是直线l上一动点,作PC⊥x轴,垂足为C,设点P的横坐标为a,若a>4,求BP的长.(用含a的代数式表示)
如图,在平面直角坐标系中,O是坐标原点,点A,B的坐标分别为(0,3),(4,0),过点B作直线l⊥AB,P是直线l上一动点,作PC⊥x轴,垂足为C,设点P的横坐标为a,若a>4,求BP的长.(用含a的代数式表示)
分析 先利用勾股定理计算出AB,再证明Rt△ABO∽Rt△BPC,然后利用相似比求PB.
解答 解:∵A(0,3),B(4,0),
∴OA=3,OB=4,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PB⊥AB,
∴∠ABO+∠PBC=90°,
∵∠ABO+∠BAO=90°,
∴∠BAO=∠PBC,
∴Rt△ABO∽Rt△BPC,
∴$\frac{OA}{BC}$=$\frac{OB}{PC}$,即$\frac{3}{a-4}$=$\frac{5}{PB}$,
∴PB=$\frac{5a-20}{3}$.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.也考查了坐标与图形性质.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
17. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠1与∠C是同位角 | B. | ∠1与∠3是对顶角 | ||
| C. | ∠3与∠C是内错角 | D. | ∠B与∠3是同旁内角 |
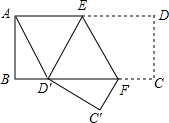 如图,四边形ABCD是矩形,AB=2,将矩形ABCD沿EF折叠,点D落在BC边的D′处.若四边形AD′FE恰好为菱形,则矩形的边AD的长度为$\frac{8\sqrt{3}}{3}$.
如图,四边形ABCD是矩形,AB=2,将矩形ABCD沿EF折叠,点D落在BC边的D′处.若四边形AD′FE恰好为菱形,则矩形的边AD的长度为$\frac{8\sqrt{3}}{3}$. (1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$
(1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$