题目内容
13.阅读下列材料,计算:56789×56786-56788×56787.解:设56786=a,则原式=a(a+3)-(a+2)(a+1)=-2.
即56789×56786-56788×56787=-2.
模仿上面的方法计算:
(1)(1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$)×($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$)-)($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$)×(1-$\frac{1}{2}$-$\frac{1}{3}$-$\frac{1}{4}$-$\frac{1}{5}$).
(2)3.1468×7.1468-0.14682.
分析 (1)设$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=a,则$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=a-$\frac{1}{5}$,代入原式将原式转化成关于a的整式化简可得结果;
(2)设0.1468=a,则3.1468=a+3,7.1468=a+7,将原式转化成关于a的整式化简可得10a+21,将a的值代入计算可得.
解答 解:(1)设$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$=a,则$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$=a-$\frac{1}{5}$,
原式=(1-a+$\frac{1}{5}$)•a-(a-$\frac{1}{5}$)(1-a)
=($\frac{6}{5}$-a)•a-(a-a2-$\frac{1}{5}$+$\frac{1}{5}$a)
=$\frac{6}{5}$a-a2-a+a2+$\frac{1}{5}$-$\frac{1}{5}$a
=$\frac{1}{5}$;
(2)设0.1468=a,则3.1468=a+3,7.1468=a+7
原式=(a+3)(a+7)-a2
=a2+10a+21-a2
=10a+21
把a=0.1468代入
原式=10×0.1468+21=22,468
∴3.1468×7.1468-0.14682=22.468.
点评 此题主要考查了整式的混合运算,要熟练掌握,解答此题的关键是要明确:有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
8. 如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
 如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )
如图,在矩形ABCD中,AB=8,BC=4,若点M、N分别是线段AC、AB上的两个动点,则BM+MN的最小值为( )| A. | 6.4 | B. | 8 | C. | 4$\sqrt{3}$ | D. | 6 |
3.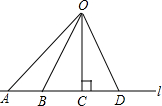 如图,下列线段中,最短的是( )
如图,下列线段中,最短的是( )
 如图,下列线段中,最短的是( )
如图,下列线段中,最短的是( )| A. | 线段OA | B. | 线段OB | C. | 线段OC | D. | 线段OD |
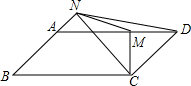 如图,在?ABCD中,AD=2AB,CM⊥AD,CN⊥AB,垂足分别为M、N,连接MN,ND.则下列结论一定正确的是①②③④.(请将序号在填在横线上)
如图,在?ABCD中,AD=2AB,CM⊥AD,CN⊥AB,垂足分别为M、N,连接MN,ND.则下列结论一定正确的是①②③④.(请将序号在填在横线上) (1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$
(1)解不等式组$\left\{\begin{array}{l}{x≤3x+2}\\{x-1<2-2x}\end{array}\right.$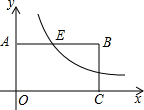 如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线y=$\frac{6}{x}$(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是24.
如图,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴上,以OA、OC为边作矩形OABC,双曲线y=$\frac{6}{x}$(x>0)交AB于点E,AE:EB=1:3.则矩形OABC的面积是24.