题目内容
1．先化简，再求值：$\frac{x-2}{{2{x^2}+4x}}÷（x+2-\frac{8x}{x+2}）$，其中x=$\sqrt{2}$+1．分析 先算括号里面的，再算除法，把x的值代入进行计算即可．
解答 解：原式=$\frac{x-2}{2x（x+2）}$÷[$\frac{{（x+2）}^{2}}{x+2}$-$\frac{8x}{x+2}$]
=$\frac{x-2}{2x（x+2）}$÷$\frac{{（x-2）}^{2}}{x+2}$
=$\frac{x-2}{2x（x+2）}$•$\frac{x+2}{{（x-2）}^{2}}$
=$\frac{1}{2x（x-2）}$，
当x=$\sqrt{2}$+1时，原式=$\frac{1}{2（\sqrt{2}+1）（\sqrt{2}+1-2）}$=$\frac{1}{2}$．
点评 本题考查的是分式的化简求值，在解答此类题目时要把分式化为最简形式，再把未知数的值代入进行计算．
练习册系列答案
阅读快车系列答案
相关题目
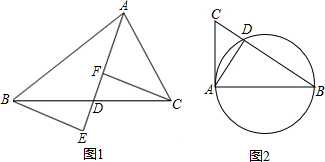
12．
在?ABCD中，过点D作对DE⊥AB于点E，点F在边CD上，CF=AE，连结AF，BF．
（1）求证：四边形BFDE是矩形．
（2）若CF=6，BF=8，DF=10，求证：AF是∠DAB的角平分线．
在?ABCD中，过点D作对DE⊥AB于点E，点F在边CD上，CF=AE，连结AF，BF．（1）求证：四边形BFDE是矩形．
（2）若CF=6，BF=8，DF=10，求证：AF是∠DAB的角平分线．
9．-2的相反数是（ ）
| A． | -2 | B． | 2 | C． | 0 |
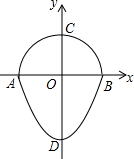如图，是一个半圆和抛物线的一部分围成的“鸭梨”，已知点A、B、C、D分别是“鸭梨”与坐标轴的交点，AB是半圆的直径，抛物线的解析式为y=2x2-2，则图中CD的长为（ ）
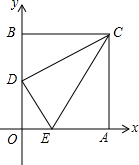如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．