题目内容
 如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是
如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是考点:垂径定理,勾股定理
专题:
分析:画出符合条件的两种极端情况,求出每种情况的弦的长,即可得出答案.
解答:解:当MN⊥OQ时,弦MN最短,如图1,

连接OM,
则∠OQM=90°,MN=2MQ,OM=5,OQ=3,
由勾股定理得:MQ=4,
即MN=8,
当MN是过Q的直径时,MN最大,此时MN=10,如图2,

所以MN长的取值范围是8≤MN≤10,
故答案为:8≤MN≤10.

连接OM,
则∠OQM=90°,MN=2MQ,OM=5,OQ=3,
由勾股定理得:MQ=4,
即MN=8,
当MN是过Q的直径时,MN最大,此时MN=10,如图2,

所以MN长的取值范围是8≤MN≤10,
故答案为:8≤MN≤10.
点评:本题考查了勾股定理,垂径定理的应用,解此题的关键是能求出最短弦和最长弦,用了分类讨论思想.

练习册系列答案
相关题目
 如图四个三角形,与如图中的三角形相似的是( )
如图四个三角形,与如图中的三角形相似的是( )A、 |
B、 |
C、 |
D、 |
下列定理中,逆命题是假命题的是( )
| A、直角三角形的两个锐角互余 |
| B、等腰三角形两腰上的高相等 |
| C、全等三角形的周长相等 |
| D、有一个锐角对应相等的两直角三角形相似 |
下列命题的逆命题是真命题的是( )
| A、如果两个角不相等,那么这两个角不是对顶角 |
| B、如果a=b,那么a2=b2 |
| C、如果两个角相等,那么这两个角是同位角 |
| D、如果一个整数能被5整除,则这个整数的个位数字是0 |
下列计算正确的是( )
| A、a5-a2=a3 |
| B、a5÷a2=a3 |
| C、a5•a2=a10 |
| D、(-a2)5=a10 |
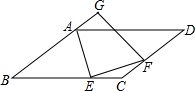 如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为
如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为 如图所示,二次函数y=ax2+bx+c(a≠0)的图象与轴交于A(-4,0)、B(1,0)两点,与y轴交于C(0,2).
如图所示,二次函数y=ax2+bx+c(a≠0)的图象与轴交于A(-4,0)、B(1,0)两点,与y轴交于C(0,2).