题目内容
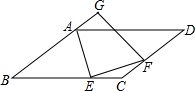 如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为
如图,?ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,延长BA到点G,使AG=CF,连接GF,若BC=7,DF=3,tan∠AEB=3,则GF的长为考点:平行四边形的性质,勾股定理,锐角三角函数的定义
专题:
分析:首先延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,进而得出FC的长,再利用勾股定理得出EH的长,即可得出FG的长.
解答: 解:延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,
解:延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,
∵AB∥DM,
∴∠M=∠BAE,∠CEM=∠DAM,
而∠BAE=∠DAM,
∴∠M=∠CEM=∠DAM,
∴CE=CM,DM=AD=7,
∵∠M+∠MFE=90°=∠CEM+∠CEF,
∴∠MFE=∠CEF,
∴CF=CE=CM=
FM=
(MD-DF)=2,
∴AB=DC=DF+CF=5,BE=BC-CE=5,
设EH=x,由
=tan∠AEB=3,
可得:AH=3x,在Rt△ABH中,AB2=AH2+BH2,
故52=(3x)2+(5-x)2,
解得:x=1,
则EH=1,AH=3,
故CH=CE+EH=3,
则AC=
=3
,
而四边形ACFG是平行四边形,
故FG=AC=3
.
故答案为:3
.
 解:延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,
解:延长AE、DC相交于点M,过点A作AH⊥BC于点H,连接AC,∵AB∥DM,
∴∠M=∠BAE,∠CEM=∠DAM,
而∠BAE=∠DAM,
∴∠M=∠CEM=∠DAM,
∴CE=CM,DM=AD=7,
∵∠M+∠MFE=90°=∠CEM+∠CEF,
∴∠MFE=∠CEF,
∴CF=CE=CM=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB=DC=DF+CF=5,BE=BC-CE=5,
设EH=x,由
| AH |
| EH |
可得:AH=3x,在Rt△ABH中,AB2=AH2+BH2,
故52=(3x)2+(5-x)2,
解得:x=1,
则EH=1,AH=3,
故CH=CE+EH=3,
则AC=
| AH2+CH2 |
| 2 |
而四边形ACFG是平行四边形,
故FG=AC=3
| 2 |
故答案为:3
| 2 |
点评:此题主要考查了平行四边形的性质以及勾股定理等知识,正确作出辅助线是解题关键.

练习册系列答案
相关题目
下列事件是必然事件的是( )
| A、有两边及一角对应相等的三角形全等 |
| B、方程x2-x+1=0有两个不等实根 |
| C、若a2=b2,则有a=b |
| D、圆的切线垂直过切点的半径 |
直角三角形的边各扩大(或缩小)相同的倍数,此三角形( )
| A、仍为直角三角形 |
| B、可能是锐角三角形 |
| C、可能是钝角三角形 |
| D、不可能是直角三角形 |
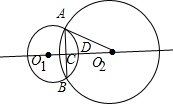 如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C=
如图,⊙O1与⊙O2相交于A、B两点,O2A切⊙O1于点A,O1O2与AB交于点C,与⊙O1交于点D.若AB=8,CD=2,则tan∠AO2C= 如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是
如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是