题目内容
已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.
考点:切线长定理,三角形的面积
专题:
分析:利用切线的性质进而利用三角形面积求法得出⊙O的半径.
解答: 解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,
解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,
连接FO,AO,OG,CO,OM,DO,OE,
四边形ABCD的面积为:
S四边形ABCD=
×EO×AD+
OM×DC+
GO×BC+
FO×AB
=
EO(AD+AB+BC+DC)
=
EO×24
=24,
解得:EO=2.
故r=2.
 解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,
解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,连接FO,AO,OG,CO,OM,DO,OE,
四边形ABCD的面积为:
S四边形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=24,
解得:EO=2.
故r=2.
点评:此题主要考查了三角形面积以及切线的性质,正确将四边形分割成三角形是解题关键.

练习册系列答案
相关题目
下列命题中,正确的是( )
| A、一组对边平行,另一组对边相等的四边形是平行四边形 |
| B、一条对角线平分一个内角的平行四边形是菱形 |
| C、两条对角线相等的四边形是矩形 |
| D、两条对角线垂直且相等的四边形是正方形 |
下列各组数为勾股数的是( )
| A、2、3、4 |
| B、8、15、16 |
| C、2.5、6、6.5 |
| D、5、12、13 |
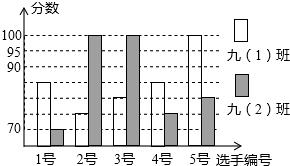 某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示. 如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是
如图,⊙O的直径为10,Q是⊙O内一点,且OQ=3,弦MN过点Q,则MN长的取值范围是 如图,AB∥CD,且CD=CB,∠D=70°,则∠ABC的度数为
如图,AB∥CD,且CD=CB,∠D=70°,则∠ABC的度数为