题目内容
17.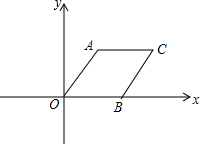 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
分析 根据题意,可分两种情况,点A在y轴正半轴或负半轴,画出图形,根据直角三角形的性质,求出点C′的坐标,点C″与C′关于原点对称.
解答  解:如图:
解:如图:
∵∠AOB=60°,把平行四边形AOBC绕点O逆时针旋转,使点A落在y轴上,
∴∠A′EC′=90°,
∵∠A′C′B=60°,
∴∠A′C′E=30°,
∵A′E=2,A′C′=4,
∴EC′=2$\sqrt{3}$,A′E=1,
∴C′(2$\sqrt{3}$,4),
∵点A′与A″关于原点对称,
∴点C″与C′关于原点对称.
∴点C″(-2$\sqrt{3}$,-4).
故答案为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);
点评 本题考查了坐标与图形的变换-旋转的性质以及勾股定理的应用,是基础知识要熟练掌握.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
7.小明有一个呈等腰三角形的积木盒,现在积木盒中只剩下如图的九个空格,下面有四种积木的搭配,其中恰好能放入的有( )
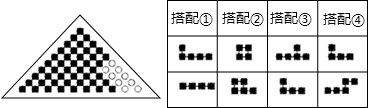

| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
12.为了提高节能意识,深圳某中学对全校的耗电情况进行了统计,他们抽查了10天中全校每天的耗电量,数据如下表:(单位:度)
(1)写出学校这10天耗电量的众数和平均数;
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.
| 度数 | 900 | 920 | 950 | 1010 | 1050 | 1100 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(2)若每度电的定价是0.8元,由上题获得的数据,估计该校每月应付电费是多少?(每月按30天计)
(3)如果做到人走电关,学校每天就可节省电量1%,按照每度电0.8元计算,写出该校节省电费y(元)与天数x(取正整数)之间的函数关系式.
2. 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )| A. | 4$\sqrt{3}$π | B. | 4$\sqrt{2}$π | C. | 2$\sqrt{3}$π | D. | 4π |
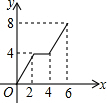
 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
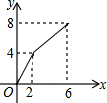
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.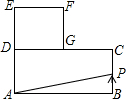 如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )
如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )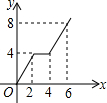
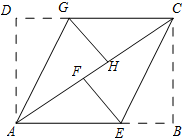 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点. 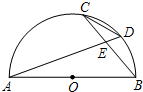 如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$.
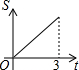
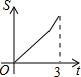
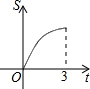
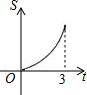
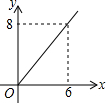
如图,AB是⊙O的直径,弦AD、BC相交于点E,若CD=5,AB=13,则sin∠BED=$\frac{12}{13}$.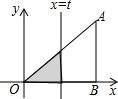 如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )
如图所示,直角三角形AOB中,AB⊥OB,且AB=OB=3.设直线l:x=t截此三角形所得的阴影部分面积为S,则S与t之间的函数关系的图象为(如选项所示)( )