题目内容
8. 甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.
甲、乙两车从A地驶向B地,甲车比乙车早行驶2h,并且在途中休息了0.5h,休息前后速度相同,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.(1)求出图中a的值;
(2)求出甲车行驶路程y(km)与时间x(h)的函数表达式,并写出相应的x的取值范围;
(3)当甲车行驶多长时间时,两车恰好相距40km.
分析 (1)求出甲的速度,根据休息前后速度相同和距离等于速度乘时间求出a的值;
(2)根据图象中自变量的取值范围分别求出各段的函数表达式;
(3)分别从甲在乙前和甲在乙后两种情况列出方程,求出时间.
解答 解:(1)由题意120÷(3.5-0.5)=40,a=1×40=40,
(2)当0≤x≤1时,设y与x之间的函数关系式为y=k1x,
把(1,40)代入,得k1=40
∴y=40x,
当$1<x≤\frac{3}{2}$时y=40;
当$\frac{3}{2}<x≤7$设y与x之间的函数关系式为y=k2x+b,由题意,得$\left\{\begin{array}{l}\frac{3}{2}{k_2}+b=40\\ \frac{7}{2}{k_2}+b=120\end{array}\right.$解得$\left\{\begin{array}{l}{k_2}=40\\ b=-20\end{array}\right.$
∴y=40x-20,
∴$y=\left\{\begin{array}{l}40x(0≤x≤1)\\ 40(1<x≤\frac{3}{2})\\ 40x-20(\frac{3}{2}<x≤7)\end{array}\right.$,
(3)设乙车行驶的路程y与时间x之间的解析式为y=k3x+b3,
由题意,得$\left\{\begin{array}{l}2{k_3}+{b_3}=0\\ \frac{7}{2}{k_3}+{b_3}=120\end{array}\right.$,解得$\left\{\begin{array}{l}{k_3}=80\\{b_3}=-160\end{array}\right.$,
∴y=80x-160,
当40x-20-(80x-160)=40时,解得:x=$\frac{5}{2}$.
当80x-160-(40x-20)=40时,解得:x=$\frac{9}{2}$.
答:甲车行驶1小时(或1-1.5小时)或$\frac{5}{2}$小时或$\frac{9}{2}$小时,两车恰好相距40km,
点评 本题考查的是一次函数的综合应用,认真观察图象,从中获取正确的信息是解题的关键,注意待定系数法在解题中的运用,和分情况讨论思想的运用.

 阅读快车系列答案
阅读快车系列答案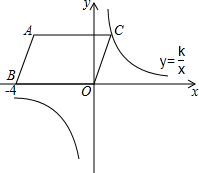 平行四边形ABOC在平面直角坐标系中,A、B的坐标分别为(-3,3),(-4,0).则过C的双曲线表达式为:y=$\frac{3}{x}$
平行四边形ABOC在平面直角坐标系中,A、B的坐标分别为(-3,3),(-4,0).则过C的双曲线表达式为:y=$\frac{3}{x}$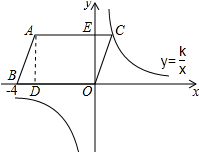 .
.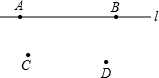 如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法)
如图,在一条笔直的高速公路I上有A、B两点,点C、D表示两个村庄,相关部门计划在高速公路的AB路段上修建一个收费站E,使得此收费站E到C、D两村庄的距离相等,请你在图中画出收费站E的位置.(保留作图痕迹,不要求写作法) 小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)
小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)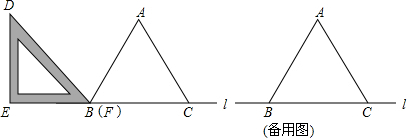

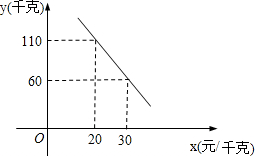 水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.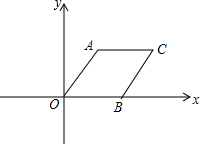 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.