题目内容
5.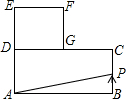 如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )
如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )| A. | 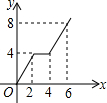 | B. | 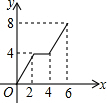 | C. | 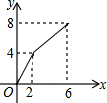 | D. | 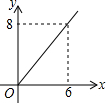 |
分析 当点P在不同线段上时,求出△PAB的面积y与x的关系式,确定函数图象.
解答 解:0≤t≤2时,
y=$\frac{1}{2}$×4×t=2t,
2≤t≤4时,
y=$\frac{1}{2}$×4×2=4,
4≤t≤6时,
y=$\frac{1}{2}$×4×(t-2)=2t-4,
∵0≤t≤6,
∴B适合.
故选:B.
点评 本题考查的是动点问题的函数图象,根据自变量的取值范围确定函数解析式是解题的关键,注意分段函数图象的画法.

练习册系列答案
相关题目
18. 如图,点A、B、C在⊙O上,若∠ABC=52°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=52°,则∠AOC的度数为( )
 如图,点A、B、C在⊙O上,若∠ABC=52°,则∠AOC的度数为( )
如图,点A、B、C在⊙O上,若∠ABC=52°,则∠AOC的度数为( )| A. | 128° | B. | 104° | C. | 50° | D. | 52° |
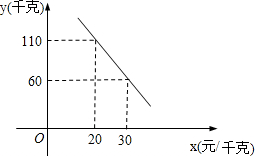
10.某工厂生产一种合金薄板(其厚度忽略不计),这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长成正比例,在营销过程中得到了表格中的数据.
(1)求一张薄板的出厂价与边长之间满足的函数关系式;
(2)40cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
(2)40cm的薄板,获得的利润是26元(利润=出厂价-成本价).
①求一张薄板的利润与边长之间满足的函数关系式;
②当边长为多少时,出厂一张薄板获得的利润最大?最大利润是多少?
 小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)
小时候,我们就用手指练习过数数,一个小朋友按如图所示的规则练习数数,数到2014时对应的指头是无名指.(注:填大拇指、食指、中指、无名指或小指)
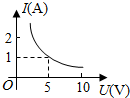

 水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.
水蜜桃是人们非常喜爱的水果之一,每年七、八月份我市水蜜桃大量上市,今年某水果商以16.5元/千克的价格购进一批水蜜桃进行销售,运输过程中质量损耗5%,运输费用是0.6元/千克,假设不计其他费用.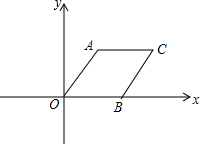 平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.
平行四边形AOBC在平面直角坐标系中的位置如图所示,∠AOC=60°,AO=2,AC=4,把平行四边形AOBC绕点O逆时针方向旋转,使点A落在y轴上,则旋转后点C的对应点C′的坐标为(2$\sqrt{3}$,4),(-2$\sqrt{3}$,-4);.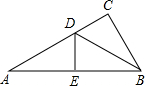 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.