题目内容
11.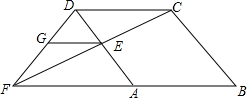 如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.
如图,已知菱形ABCD中,在AD上任取一点E,连结CE并延长与BA的延长线交于点F,过E作EG∥FB交FD于G,求证:GF=AE.
分析 根据相似三角形的判定和性质进行分析证明即可.
解答 解:∵菱形ABCD,
∴AD‖BC,FB‖CD,
∴△FAE∽FBC,
∴$\frac{AE}{BC}=\frac{EF}{FC}$,
∵EG‖FB,
∴EG‖CD,
∴△FEG∽△FCD,
∴$\frac{EG}{CD}=\frac{EF}{FC}$,
∴$\frac{EG}{CD}=\frac{AE}{BC}$,
∵CD=BC(菱形四边相等),
∴FG=AE.
点评 此题考查菱形的性质,关键是根据相似三角形的判定和性质进行分析.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
1.下列算式中,正确的有( )
| A. | $\sqrt{3}$+$\sqrt{4}$=$\sqrt{7}$ | B. | 3$\sqrt{2}$-2$\sqrt{2}$=-$\sqrt{2}$ | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{1\frac{1}{2}}$÷$\sqrt{\frac{1}{6}}$=3 |
16.下列各数中,比-2大的数是( )
| A. | -3 | B. | 0 | C. | -2 | D. | -2.1 |
 在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2);
在平面直角坐标系中,描出下列3个点:A (-1,0),把点A向右平移2个单位,再向上平移4个单位得到点B,点C 的坐标是(4,2); 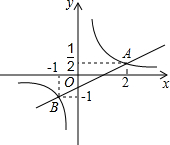 如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点.
如图,平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)图象相交于A、B两点. 如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(4,0),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC中点,则k的值是3$\sqrt{3}$.
如图所示,等边三角形ABC放置在平面直角坐标系中,已知A(0,0)、B(4,0),反比例函数y=$\frac{k}{x}$(k>0)的图象经过BC中点,则k的值是3$\sqrt{3}$. 如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草.
如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草.