题目内容
15.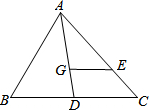 如图,点G为△ABC的重心,GE∥BC,BC=12,则GE=4.
如图,点G为△ABC的重心,GE∥BC,BC=12,则GE=4.
分析 首先根据G点为△ABC的重心,判断出AG:AD=2:3;然后根据平行线的性质,判断出$\frac{GE}{CD}=\frac{AG}{AD}$=$\frac{2}{3}$,即可求出GE的值是多少.
解答 解:∵点G点为△ABC的重心,
∴CD=$\frac{1}{2}$BC=$\frac{1}{2}$×12=6;
∴AG:GD=2:1,
∴AG:AD=2:3,
又∵GE∥BC,
∴$\frac{GE}{CD}=\frac{AG}{AD}$=$\frac{2}{3}$,
∴GE=$\frac{2}{3}$CD=$\frac{2}{3}×6$=4.
故答案为:4.
点评 此题主要考查了三角形的重心的性质和应用,要熟练掌握,解答此题的关键是要明确:①重心到顶点的距离与重心到对边中点的距离之比为2:1.②重心和三角形3个顶点组成的3个三角形面积相等.③重心到三角形3个顶点距离的和最小.

练习册系列答案
相关题目
10. 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
 如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )
如图,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则△ABC的面积是( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
20.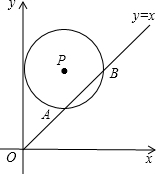 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
5.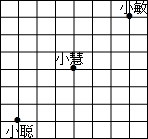 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
 课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )
课间操时,小聪、小慧、小敏的位置如图所示,小聪对小慧说,如果我的位置用(1,1)表示,小敏的位置用(7,7)表示,那么你的位置可以表示成( )| A. | (5,4) | B. | (4,4) | C. | (3,4) | D. | (4,3) |
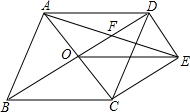 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE交OD于点F.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=$\frac{1}{2}$AC,连接CE、OE,连接AE交OD于点F.