Question

11．边长为2的等边三角形ABC，绕点A旋转120°，则BC边上的中点D转过的路程是$\frac{2\sqrt{3}}{3}$π．

Answer 1

分析 首先利用勾股定理可求出AD的长，由题意可知BC边上的中点D转过的路程是以点A为圆心，AD的长为半径，圆心角为120°的弧长，所以利用弧长公式计算即可．

解答 解：
∵△ABC是等边三角形，
∴AB=AC=BC=2，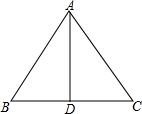
∵BD=CD，
∴AD⊥BC，
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{3}$，
∵绕点A旋转120°，
∴BC边上的中点D转过的路程=$\frac{120×π×\sqrt{3}}{180}$=$\frac{2\sqrt{3}}{3}$π，
故答案为：$\frac{2\sqrt{3}}{3}$π．

点评 本题考查了旋转的性质、等边三角形的性质以及勾股定理的运用和弧长公式的运用，熟记等边三角形的各种性质是解题的关键．