题目内容
14.a,b,c为常数,且(a-c)2>a2+c2,则关于x的方程ax2+bx+c=0根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
分析 利用完全平方的展开式将(a-c)2展开,即可得出ac<0,再结合方程ax2+bx+c=0根的判别式△=b2-4ac,即可得出△>0,由此即可得出结论.
解答 解:∵(a-c)2=a2+c2-2ac>a2+c2,
∴ac<0.
在方程ax2+bx+c=0中,
△=b2-4ac≥-4ac>0,
∴方程ax2+bx+c=0有两个不相等的实数根.
故选B.
点评 本题考查了完全平方公式以及根的判别式,解题的关键是找出△=b2-4ac>0.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式的符号,得出方程实数根的个数是关键.

练习册系列答案
相关题目
2.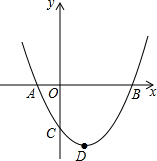 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )| A. | 2a-b=0 | B. | a+b+c>0 | ||
| C. | 3a-c=0 | D. | 当a=$\frac{1}{2}$时,△ABD是等腰直角三角形 |
9.若$\frac{1}{x+1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>-1 | C. | x≠-1 | D. | x<-1 |
19.下列运算正确的是( )
| A. | (-$\frac{3}{2}$)2=-$\frac{9}{4}$ | B. | (3a2)3=9a6 | C. | 5-3÷5-5=$\frac{1}{25}$ | D. | $\sqrt{8}-\sqrt{50}=-3\sqrt{2}$ |
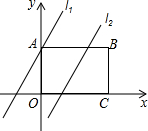 如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x-3.
如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x-3.
 一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )