题目内容
2.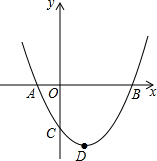 如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )
如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为-1和3,则下列结论正确的是( )| A. | 2a-b=0 | B. | a+b+c>0 | ||
| C. | 3a-c=0 | D. | 当a=$\frac{1}{2}$时,△ABD是等腰直角三角形 |
分析 由于抛物线与x轴的交点A、B的横坐标分别为-1,3,得到对称轴为直线x=1,则-$\frac{b}{2a}$=1,即2a+b=0,得出,选项A错误;
当x=1时,y<0,得出a+b+c<0,得出选项B错误;
当x=-1时,y=0,即a-b+c=0,而b=-2a,可得到a与c的关系,得出选项C错误;
由a=$\frac{1}{2}$,则b=-1,c=-$\frac{3}{2}$,对称轴x=1与x轴的交点为E,先求出顶点D的坐标,由三角形边的关系得出△ADE和△BDE都为等腰直角三角形,得出选项D正确;即可得出结论.
解答 解:∵抛物线与x轴的交点A、B的横坐标分别为-1,3,
∴抛物线的对称轴为直线x=1,则-$\frac{b}{2a}$=1,
∴2a+b=0,
∴选项A错误;
∴当自变量取1时,对应的函数图象在x轴下方,
∴x=1时,y<0,则a+b+c<0,
∴选项B错误;
∵A点坐标为(-1,0),
∴a-b+c=0,而b=-2a,
∴a+2a+c=0,
∴3a+c=0,
∴选项C错误;
当a=$\frac{1}{2}$,则b=-1,c=-$\frac{3}{2}$,对称轴x=1与x轴的交点为E,如图,
∴抛物线的解析式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
把x=1代入得y=$\frac{1}{2}$-1-$\frac{3}{2}$=-2,
∴D点坐标为(1,-2),
∴AE=2,BE=2,DE=2,
∴△ADE和△BDE都为等腰直角三角形,
∴△ADB为等腰直角三角形,
∴选项D正确.
故选D.
点评 本题考查了二次函数y=ax2+bx+c的图象与系数的关系:当a>0,抛物线开口向上;抛物线的对称轴为直线x=-$\frac{b}{2a}$;抛物线与y轴的交点坐标为(0,c).

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案| A. |  | B. |  | C. |  | D. |  |
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 1.2×10-9米 | D. | 12×10-8米 |
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
| A. | y=2x2-4 | B. | y=2(x-2)2 | C. | y=2x2+2 | D. | y=2(x+2)2 |
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
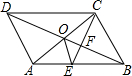 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论: