题目内容
6. 一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )
一次函数y=ax+b和反比例函数y=$\frac{c}{x}$在同一平面直角坐标系中的图象如图所示,则二次函数y=ax2+bx+c的图象大致为( )| A. |  | B. |  | C. | 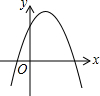 | D. |  |
分析 根据一次函数的图象的性质先确定出a、b的取值范围,然后根据反比例函数的性质确定出c的取值范围,最后根据二次函数的性质即可做出判断.
解答 解:∵一次函数y=ax+b经过一、二、四象限,
∴a<0,b>0,
∵反比例函数y=$\frac{c}{x}$的图象在一、三象限,
∴c>0,
∵a<0,
∴二次函数y=ax2+bx+c的图象的开口向下,
∵b>0,
∴$-\frac{b}{2a}$>0,
∵c>0,
∴与y轴的正半轴相交,
故选C.
点评 本题主要考查的是二次函数、一次函数和反比例函数的性质,掌握相关性质是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
17.关于x的一元二次方程x2-$\sqrt{2}$x+sinα=0有两个相等的实数根,则锐角α等于( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
14.a,b,c为常数,且(a-c)2>a2+c2,则关于x的方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
1.下列各式计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | x2•x3=x6 | C. | x2+x3=x5 | D. | (a3)3=a9 |
16.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,-1) |

 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.