题目内容
5.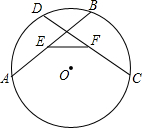 如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.
如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.
分析 利用同圆或等圆中相等的弦所对的弧、弦心距相等可得EO=FO,进而得到∠OEF=∠OFE,从而可得∠AEO-∠FEO=∠CFO-∠OFE,进而得到∠AEF=∠CFE;
解答 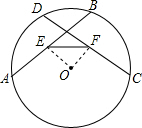 证明:连接OE,OF,
证明:连接OE,OF,
∵点E、F是AB、CD的中点,
∴EO⊥AB,FO⊥CD,
∴∠AEO=∠CFO=90°,
∵OE⊥AB于E,OF⊥CD于F,
∴OE和OF是圆的两条弦的弦心距,
∵AB,CD是⊙O的两条弦,AB=CD,
∴EO=FO,
∴∠OEF=∠OFE,
∵OE⊥AB于E,OF⊥CD于F,
∴∠AEO=∠CFO=90°,
∴90°+∠FEO=90°+∠OFE,
即:∠AEF=∠CFE.
点评 本题考查了垂径定理,圆心角、弧、弦的关系,解题的关键是正确的将证明弦心距转化为证明两弦相等.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
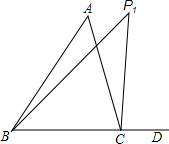 如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP3、CP3相交于点P3,∠P3BC=n∠ABP3,∠P3CD=n∠ACP3,直接写出∠A、∠P3之间满足的数量关系:∠A=$\frac{n+1}{n}$∠P3.
如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP3、CP3相交于点P3,∠P3BC=n∠ABP3,∠P3CD=n∠ACP3,直接写出∠A、∠P3之间满足的数量关系:∠A=$\frac{n+1}{n}$∠P3.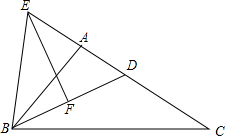 已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.
已知,在△ABC中,BD平分∠ABC,EF垂直平分BD交CA延长线于E,求证:∠EBA=∠C.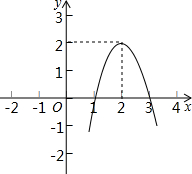 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: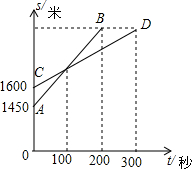 一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米,此后两人分别以a米/秒和b米/秒匀速跑,两人匀速跑的路程S米与时间t秒的关系如图所示,结合图象求出这次越野跑的全程为多少米?
一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米,此后两人分别以a米/秒和b米/秒匀速跑,两人匀速跑的路程S米与时间t秒的关系如图所示,结合图象求出这次越野跑的全程为多少米?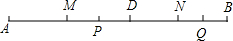 如图,D是线段AB上一点,M是AD的中点,N是DB的中点,P是MD的中点,Q是NB的中点,已知线段PQ=10,DQ=6,求线段AB的长.
如图,D是线段AB上一点,M是AD的中点,N是DB的中点,P是MD的中点,Q是NB的中点,已知线段PQ=10,DQ=6,求线段AB的长.