题目内容
17.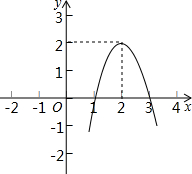 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,求k取值范围.
分析 (1)根据图象可知x=1和3是方程的两根;
(2)找出函数值大于0时x的取值范围即可;
(3)首先找出对称轴,然后根据图象写出y随x的增大而减小的自变量x的取值范围;
(4)若方程ax2+bx+c=k有两个不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,据此求出k的取值范围.
解答 解:(1)由图象可知,图象与x轴交于(1,0)和(3,0)点,则方程ax2+bx+c=0的两个根为1和3;
(2)由图象可知当1<x<3时,不等式ax2+bx+c>0;
(3)由图象可知,y=ax2+bx+c(a≠0)的图象的对称轴为x=2,开口向下,
即当x>2时,y随x的增大而减小;
(4)由图象可知,二次函数y=ax2+bx+c(a≠0)的最大值为2,
若方程ax2+bx+c=k有两个不相等的实数根,则k必须小于y=ax2+bx+c(a≠0)的最大值,
则k<2.
点评 本题主要考查了二次函数与不等式以及抛物线与x轴的交点的知识,解答本题的关键是熟练掌握二次函数的性质以及图象的特点,此题难度不大.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.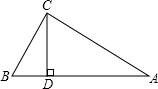 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )
如图,在△ABC中,∠ACB=90°,∠A=30°,AB=2$\sqrt{5}$,CD是AB边上的高.则BD等于( )| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | $\frac{2\sqrt{5}}{3}$ |
6.我们把5个一元硬币摞在一起测得高度大约为1cm,那么10万个这样的硬币摞在一起,其高度最接近于( )
| A. | 地球赤道的长度 | B. | 地球半径的长度 | ||
| C. | 70层大厦的高度 | D. | 学校操场国旗旗杆的高度 |
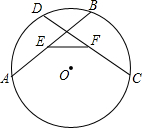 如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.
如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.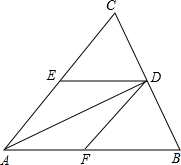 如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.
如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.