题目内容
20.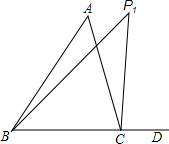 如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP3、CP3相交于点P3,∠P3BC=n∠ABP3,∠P3CD=n∠ACP3,直接写出∠A、∠P3之间满足的数量关系:∠A=$\frac{n+1}{n}$∠P3.
如图,分别在△ABC的一个内角∠ABC和一个外角∠ACD内部作射线BP3、CP3相交于点P3,∠P3BC=n∠ABP3,∠P3CD=n∠ACP3,直接写出∠A、∠P3之间满足的数量关系:∠A=$\frac{n+1}{n}$∠P3.
分析 设∠ABP2=x,∠ACP2=y,根据三角形外角的性质列出算式,整理得到答案.
解答 解:设∠ABP3=x,∠ACP3=y,
则∠CBP3=nx,∠DCP3=ny,
∵∠ACD=∠A+∠ABC,即(1+n)y=∠A+(1+n)x,
∠P3CD=∠P3+∠CBP3,即ny=∠P3+nx,
解得:n∠A=(n+1)∠P3,
∴∠A=$\frac{n+1}{n}$∠P3,
故答案为:∠A=$\frac{n+1}{n}$∠P3.
点评 本题考查的是三角形的外角的性质,掌握三角形的一个外角等于与它不相邻的两个内角的和是解题的关键.

练习册系列答案
相关题目
10.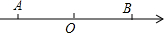 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
 如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )
如图,数轴上两点A,B到原点O的距离相等,如果点A,B表示的数分别是x+3和x+7,那么线段OA的长度是( )| A. | 2 | B. | x+5 | C. | -2 | D. | 4 |
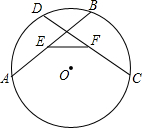 如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.
如图,在⊙O中,弦AB=CD,E、F分别为AB、CD的中点,求证:∠AEF=∠CFE.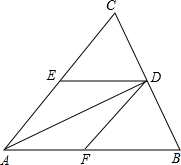 如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.
如图,AD是△ABC的角平分线,DE∥AB,DF∥AC,分别交AC,AB于点E,F.若∠EAD=20°,求∠EDF的度数.