题目内容
8. 如图,AB、CD相交于O,OE⊥AB,若∠EOD=70°,则∠AOC=20°.
如图,AB、CD相交于O,OE⊥AB,若∠EOD=70°,则∠AOC=20°.
分析 根据垂直的定义可得∠BOE=90°,然后求出∠BOD,再根据对顶角相等可得∠AOC=∠BOD.
解答 解:∵OE⊥AB,
∴∠BOE=90°,
∴∠BOD=90°-∠EOD=90°-70°=25°,
∴∠AOC=∠BOD=20°,
故答案为:20.
点评 本题考查了对顶角相等的性质,以及垂直的定义,熟记概念与性质并准确识图是解题的关键.

练习册系列答案
相关题目
3.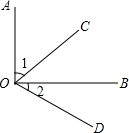 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
 如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )
如图,如果∠AOB=∠COD=90°,那么∠1=∠2,这是根据( )| A. | 直角都相等 | B. | 等角的余角相等 | C. | 同角的余角相等 | D. | 同角的补角相等 |
20.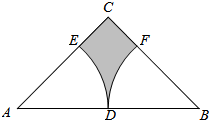 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD、扇形FBD的圆心分别为点A、点B、且AB=4,则图中阴影部分的面积为( )| A. | 2-π | B. | 3-π | C. | 3.5-π | D. | 4-π |
18.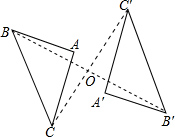 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |

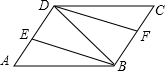 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.