题目内容
7. 已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.
已知:如图,点E、F分别为平行四边形ABCD的BC、AD边上的点,且∠1=∠2.求证:AE=FC.
分析 根据平行四边形的对边相等,对角相等,易得△ABE≌△CDF,即可得AE=CF.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠B=∠D.
在△ABE与△CDF中,
$\left\{\begin{array}{l}{∠1=∠2}\\{AB=CD}\\{∠B=∠D}\end{array}\right.$
∴△ABE≌△CDF(ASA).
∴AE=CF.
点评 此题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等.还考查了全等三角形的判定与性质.此题比较简单,解题要细心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.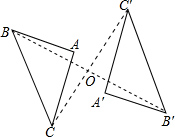 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
 如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )
如图,已知△ABC与△A′B′C′关于点O成中心对称图形,则下列判断不正确的是( )| A. | ∠ABC=∠A′B′C′ | B. | ∠BOC=∠B′A′C′ | C. | AB=A′B′ | D. | OA=OA′ |
12. 如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
 如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )
如图所示,如果△AOB与△AOD的周长之差为8,而AB:AD=3:2,那么?ABCD的周长( )| A. | 16 | B. | 24 | C. | 40 | D. | 80 |
16.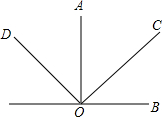 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
 如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )
如图,OA⊥OB,OC⊥OD,∠AOC=α,那么∠B0D等于( )| A. | 180°-2α | B. | 180°-α | C. | 90°+$\frac{1}{2}$α | D. | 2α-90° |
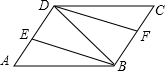 如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F.
如图,在?ABCD中,连接对角线BD,BE平分∠ABD交AD于点E,DF平分∠BDC交BC于点F. 画出该几何体的三视图:
画出该几何体的三视图: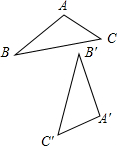 已知△A′B′C′是由△ABC经过顺时针旋转而得.
已知△A′B′C′是由△ABC经过顺时针旋转而得.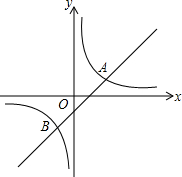 如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)
如图,直线y=x+b和双曲线$y=\frac{k}{x}$相交于点A、B,且点A坐标为(2,1)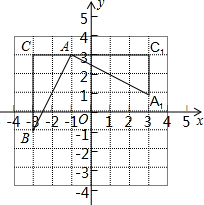 如图,在平面直角坐标系中,A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.