题目内容
8. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.
如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.(1)求证:四边形AFCE是菱形;
(2)若AB=4,BC=8,求菱形AFCE的边长.
分析 (1)根据ABCD为矩形,根据矩形的对边平行得到AE与CF平行,由两直线平行得到一对内错角相等,又EF垂直平分AC,根据垂直平分线的定义得到AO=CO,且AC与EF垂直,再加上一对对顶角相等,利用“ASA”得到三角形AOE与三角形COF全等,根据全等三角形的对应边相等得到AE=FC,由一组对边平行且相等的四边形为平行四边形得到AFCE为平行四边形,又根据对角线垂直的平行四边形为菱形即可得证;
(2)由矩形的性质得到∠B为直角,在直角三角形ABC中,由AB与BC的长,利用勾股定理求出AC的长,又已知EF的长,而AC与EF为菱形AFCE的两条对角线,根据对角线乘积的一半即可求出菱形的面积.
解答 解:(1)∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DAC=∠BCA,∠AEF=∠CFE,
∵EF垂直平分对角线AC,
∴OA=OC,EF⊥EC,
∴△AOE≌△COF,
∴OA=OC,OE=OF,
∴四边形AFCE是平行四边形,
∵∠AOF=90°,
∴四边形AFCE是菱形;
(2)∵四边形AFCE是菱形,
∴AF=FC,
在Rt△ABF中,设AF=FC=x,则BF=8-x
∴AB2+BF2=AF2,
∴42+(8-x)2=x2,
∴x=5,
∴菱形AFCE的边长等于5.
点评 此题考查了矩形的性质,菱形的判定与性质,以及勾股定理.其中矩形的性质有对边平行且相等,四个角都为直角,对角线互相平行且相等;菱形的性质有四条边相等,对角线互相平分且垂直,一条对角线平分一组对角;菱形的判定方法一般有:四条边相等的四边形为菱形,对角线互相垂直的平行四边形为菱形,邻边相等的平行四边形为菱形等,熟练掌握这些判定与性质是解本题的关键.同时注意菱形的面积可以利用对角线乘积的一半来求.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
13.下列二次根式中属于最简二次根式的是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{\frac{a}{b}}$ | C. | $\sqrt{{a}^{2}+1}$ | D. | $\sqrt{4a+4}$ |
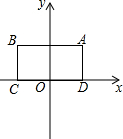 对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.
对于⊙P及一个矩形给出如下定义:如果⊙P上存在到此矩形四个顶点距离都相等的点,那么称⊙P是该矩形的“等距圆”.如图,在平面直角坐标系xOy中,矩形ABCD的顶点A的坐标为($\sqrt{3}$,2),顶点C、D在x轴上,且OC=OD.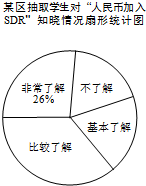 “世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表:
“世界那么大,我想去看看”一句话红遍网络,随着国际货币基金组织正式宣布人民币2016年10月1日加入SDR(特别提款权),以后出国看世界更加方便.为了解某区6000名初中生对“人民币加入SDR”知晓的情况,某校数学兴趣小组随机抽取区内部分初中生进行问卷调查,将问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不了解”四个等级,并将调查结果整理分析,得到下列图表: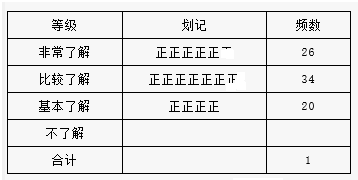
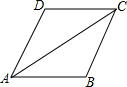 如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.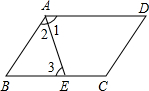 如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长.
如图所示,在平行四边形ABCD中,∠BAD的平分线AE分对边长度为3和4两部分,求四边形ABCD的周长.