题目内容
3.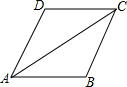 如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=∠D,∠DCA=∠CAB,求证:四边形ABCD是平行四边形.
分析 根据三角形内角和为180°可得∠DAC=∠ACB,根据等式的性质可得∠DAC+∠CAB=∠ACB+∠DCA,进而可得∠DAB=∠DCB,根据两组对角分别相等的四边形是平行四边形可得结论.
解答 证明:∵∠B=∠D,∠DCA=∠CAB,
∴∠DAC=∠ACB,
∴∠DAC+∠CAB=∠ACB+∠DCA,
∴∠DAB=∠DCB,
∵∠B=∠D,
∴四边形ABCD是平行四边形.
点评 此题主要考查了平行四边形的判定,关键是掌握两组对角分别相等的四边形是平行四边形.

练习册系列答案
相关题目
15.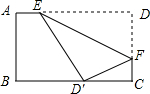 如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为( )
如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为( )
 如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为( )
如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 1 |
13.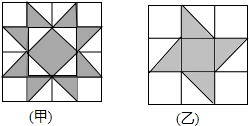 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则( )
如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则( )
 如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则( )
如图,有甲、乙两种地板样式,如果小球分别在上面自由滚动,设小球在甲种地板上最终停留在黑色区域的概率为P1,在乙种地板上最终停留在黑色区域的概率为P2,则( )| A. | P1>P2 | B. | P1<P2 | C. | P1=P2 | D. | 以上都有可能 |
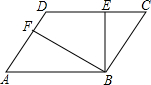 如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则?ABCD的周长为20.
如图,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别为E,F,CE=2,DF=1,∠EBF=60°,则?ABCD的周长为20.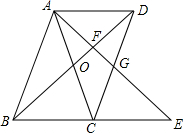 如图,?ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G.
如图,?ABCD中,AC与BD相交于点O,AB=AC,延长BC到点E,使CE=BC,连接AE,分别交BD、CD于点F、G. 如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.
如图,在矩形ABCD中,对角线AC的垂直平分线EF分别与边AD、BC相交于E、F,垂足为O,连接AF、CE.