题目内容
9．点P（4，3）到原点的距离是（ ）| A． | 3 | B． | 4 | C． | 5 | D． | 7 |
分析 先画图，根据图可知道OA=4，AP=3，再利用勾股定理可求OP．
解答 解：如图所示，
∵P点坐标是（4，3），
∴OA=4，AP=OB=3，
∴OP=$\sqrt{O{A}^{2}+A{P}^{2}}$=5．
故选：C．
点评 本题主要考查勾股定理，解答本题的关键是熟练掌握勾股定理的知识点，此题比较简单．注意数形思想的应用．
练习册系列答案
相关题目
19．
如图，四边形ABCD是平行四边形，O是对角线AC与BD的交点，AB⊥AC，若AB=8，AC=12，则BD的长是（ ）
如图，四边形ABCD是平行四边形，O是对角线AC与BD的交点，AB⊥AC，若AB=8，AC=12，则BD的长是（ ）| A． | 16 | B． | 18 | C． | 20 | D． | 22 |
17．计算（$\sqrt{2}$）2的结果是（ ）
| A． | 4 | B． | ±2 | C． | -2 | D． | 2 |
14．
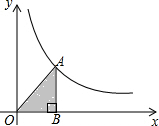如图，在直角坐标系中，点A是双曲线y=$\frac{3}{x}$（x＞0）上的一个动点，过点A作AB⊥x轴于点B．当点A的横坐标逐渐增大时，△OAB的面积将会（ ）
如图，在直角坐标系中，点A是双曲线y=$\frac{3}{x}$（x＞0）上的一个动点，过点A作AB⊥x轴于点B．当点A的横坐标逐渐增大时，△OAB的面积将会（ ）| A． | 逐渐增大 | B． | 不变 | C． | 先增大后减小 | D． | 逐渐减小 |