题目内容
18．解方程：$\left\{\begin{array}{l}{2x-3y-2=0}\\{3y+x=1}\end{array}\right.$．分析 方程组整理后，利用加减消元法求出解即可．
解答 解：方程组整理得：$\left\{\begin{array}{l}{2x-3y=2①}\\{x+3y=1②}\end{array}\right.$，
①+②得：3x=3，即x=1，
把x=1代入②得：y=0，
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$．
点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
练习册系列答案
名校课堂系列答案
相关题目
9．点P（4，3）到原点的距离是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 7 |
13．下列说法错误的是（ ）
| A． | 若△ABC中，a2=（b+c）（b-c），则△ABC是直角三角形 | |
| B． | 若△ABC中，a2+b2≠c2，则△ABC不是直角三角形 | |
| C． | 若△ABC中，a：b：c=13：5：12，则∠A=90° | |
| D． | 若△ABC中，a、b、c三边的长分别为n2-1、2n、n2+1（n＞1），则△ABC是直角三角形 |
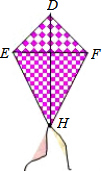为参加学校举办的风筝设计比赛，小明用四根竹棒扎成如图所示的风筝框架，其中∠EDH=∠FDH，ED=FD．将上述条件标注在图中，小明不用测量就能知道EH=FH吗？为什么？