题目内容
19. 如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )
如图,四边形ABCD是平行四边形,O是对角线AC与BD的交点,AB⊥AC,若AB=8,AC=12,则BD的长是( )| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
分析 由四边形ABCD是平行四边形,根据平行四边形的对角线互相平分,可得OA的长,然后由AB⊥AC,AB=8,AC=12,根据勾股定理可求得OB的长,继而求得答案.
解答 解:∵四边形ABCD是平行四边形,AC=12,
∴OA=$\frac{1}{2}$AC=6,BD=2OB,
∵AB⊥AC,AB=8,
∴OB=$\sqrt{O{A}^{2}+A{B}^{2}}$=10,
∴BD=2OB=20.
故选C.
点评 此题考查了平行四边形的性质以及勾股定理.注意掌握平行四边形的对角线互相平分.

练习册系列答案
相关题目
9.某餐饮公司为一所学校提供午餐,有10元、12元、15元三种价格的盒饭供师生选择,每人选一份,该校师生某一天购买的这三种价格盒饭数依次占50%、30%、20%,那么这一天该校师生购买盒饭费用的平均数和中位数分别是( )
| A. | 12元、12元 | B. | 12元、11元 | C. | 11.6元、12元 | D. | 11.6元、11元 |
14.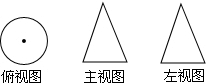 如图所示某几何体的三视图,则这个几何体是( )
如图所示某几何体的三视图,则这个几何体是( )
 如图所示某几何体的三视图,则这个几何体是( )
如图所示某几何体的三视图,则这个几何体是( )| A. | 三棱锥 | B. | 圆柱 | C. | 球 | D. | 圆锥 |
4.已知△ABC的三个内角满足,∠B+∠C=2∠A,则∠A的度数为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
9.点P(4,3)到原点的距离是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
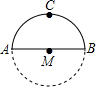 如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )
如图,李老师早晨出门去锻炼,一段时间内沿⊙M的半圆形M→A→C→B→M路径匀速慢跑,那么李老师离出发点M的距离与时间x之间的函数关系的大致图象是( )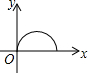



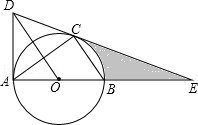 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.
如图,是可以自由转动的转盘,该转盘被分成6个相等的扇形区域.