题目内容
4．平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分，则该平行四边形的周长为14cm或16cm．分析 根据题意画出图形，由平行四边形得出对边平行，又由角平分线可以得出△ABE为等腰三角形，然后分别讨论BE=2cm，CE=3cm或BE=3cm，CE=2cm，继而求得答案．
解答 解：如图，∵四边形ABCD为平行四边形，
∴AD∥BC，
∴∠DAE=∠AEB，
∵AE为角平分线，
∴∠DAE=∠BAE，
∴∠AEB=∠BAE，
∴AB=BE，
∴①当AB=BE=2cm，CE=3cm时，
则周长为14cm；
②当AB=BE=3cm时，CE=2cm，
则周长为16cm．
故答案为：14cm或16cm．
点评 此题考查了平行四边形的性质以及等腰三角形的判定与性质．注意分类讨论思想的应用．
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
14．
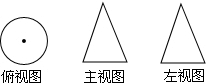如图所示某几何体的三视图，则这个几何体是（ ）
如图所示某几何体的三视图，则这个几何体是（ ）| A． | 三棱锥 | B． | 圆柱 | C． | 球 | D． | 圆锥 |
19．下列各组数能成为直角三角形三边的是（ ）
| A． | 32、42、52 | B． | $\frac{1}{3}$、$\frac{1}{4}$、$\frac{1}{5}$ | C． | $\sqrt{3}$、2、$\sqrt{5}$ | D． | $\frac{3}{5}$、$\frac{4}{5}$、1 |
9．点P（4，3）到原点的距离是（ ）
| A． | 3 | B． | 4 | C． | 5 | D． | 7 |
16．
平行四边形ABCD与等边△AEF如图放置，如果∠B=45°，则∠BAE的大小是（ ）
平行四边形ABCD与等边△AEF如图放置，如果∠B=45°，则∠BAE的大小是（ ）| A． | 75° | B． | 70° | C． | 65° | D． | 60° |
13．下列说法错误的是（ ）
| A． | 若△ABC中，a2=（b+c）（b-c），则△ABC是直角三角形 | |
| B． | 若△ABC中，a2+b2≠c2，则△ABC不是直角三角形 | |
| C． | 若△ABC中，a：b：c=13：5：12，则∠A=90° | |
| D． | 若△ABC中，a、b、c三边的长分别为n2-1、2n、n2+1（n＞1），则△ABC是直角三角形 |
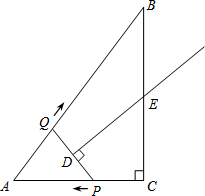如图，在Rt△ABC中，∠C=90°，AC=3，AB=5．点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动；点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动．伴随着P、Q的运动，DE保持垂直平分PQ，且交PQ于点D，交BC于点E．点P、Q同时出发，当点P到达点A时停止运动，点Q也随之停止．设点P、Q运动的时间是t秒（t＞0）．