题目内容
16. 如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
分析 设C(a,2a+2),根据已知求得D的横坐标与C的横坐标的关系,从而表示出D(-$\frac{3}{2}$a,-3a+2),根据反比例函数图象上点的坐标特征得出a(2a+2)=-$\frac{3}{2}$a(-3a+2),解得,a1=2,a2=0(舍去),从而求得C(2,6),进而即可求得k的值.
解答 解:设C(a,2a+2),
∵3S△ACO=2S△ADO,
∴3×$\frac{1}{2}$OA•a=2×$\frac{1}{2}$OA•|xD|,
∴|xD|=$\frac{3}{2}$a,
∴D(-$\frac{3}{2}$a,-3a+2),
∵C、D是双曲线y=$\frac{k}{x}$上点,
∴a(2a+2)=-$\frac{3}{2}$a(-3a+2),
解得,a1=2,a2=0(舍去),
∴C(2,6),
∴k=2×6=12.
点评 本题主要考查反比例函数和一次函数的交点问题,解答本题的关键是熟练掌握反比例函数的性质以及反比例函数图象的特征,此题难度不大,是一道不错的试题.

练习册系列答案
相关题目
7.立方根等于本身的数是( )
| A. | 1 | B. | 0 | C. | ±1 | D. | ±1.0 |
5.观察下列一组图形,它反映了图中点的个数与第n图形之间的某种变化规律,
(1)填写下表:
(2)设第n个图形中点的个数为S个,试写出S与n的关系式S=$\frac{1}{2}$(n+1)(n+2);
(3)求出第10个图形中S的值.

(1)填写下表:
| 第n个图形 | 1 | 2 | 3 | 4 |
| 图中所有点的个数 | 3 | 6 | 10 | 15 |
(3)求出第10个图形中S的值.

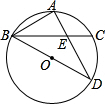 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.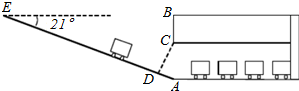 某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43)
某校九年级数学兴趣小组为了测得该校地下停车场的限高CD,在课外活动时间测得下列数据:如图,从地面E点测得地下停车场的俯角为21°,斜坡AE的长为20米,地面B点(与E点在同一个水平线)距停车场顶部C点(A、C、B在同一条直线上且与水平线垂直)1.6米.试求该校地下停车场的高度AC及限高CD(结果精确到0.1米).(参考数据:sin21°≈0.28,cos21°≈0.91,tan21°≈0.43) 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.