题目内容
6.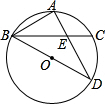 如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4.(1)判断△ABE与△ADB是否相似,并说明理由;
(2)求∠C的度数.
分析 (1)根据已知条件可以推出弧AB与弧AC相等,所以∠ABC=∠ADB,结合图形,即可推出△ABE∽△ABD,
(2)根据相似三角形的性质,就可推出AB的长度,根据直角三角形的性质求出∠C.
解答  (1)证明:如图,连接AC,
(1)证明:如图,连接AC,
∵点A是弧BC的中点,
∴∠ABC=∠ACB,
又∵∠ACB=∠ADB,
∴∠ABC=∠ADB.
又∵∠BAE=∠BAE,
∴△ABE∽△ABD;
(2)解:∵AE=2,ED=4,
∴AD=AE+ED=2+4=6,
∵△ABE∽△ABD,BD为⊙O的直径,
∴∠BAD=90°,
∵△ABE∽△ABD,
∴$\frac{AE}{AB}$=$\frac{AB}{AD}$,
∴AB2=AE•AD=2×6=12,
∴AB=2$\sqrt{3}$,
在Rt△ADB中,AB=2$\sqrt{3}$,AE=2,
∴∠ABE=30°,
∵AB=AC,
∴∠C=∠ABE=30°.
点评 本题主要考查相似三角形的判定和性质、圆周角定理、锐角三角函数的定义,关键在于找到相似三角形,根据相关的定理求出有关边的长度.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
16.$\frac{1}{4}$的算术平方根是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | ${\;}_{-}^{+}$$\frac{1}{2}$ | D. | $\frac{1}{16}$ |
17.在?ABCD中,∠A:∠B:∠C:∠D的值可能是( )
| A. | 1:2:3:4 | B. | 1:2:1:2 | C. | 2:2:1:1 | D. | 1:2:2:1 |
18.以下说法正确的是( )
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
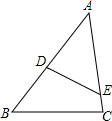 如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5.
如图,在△ABC中,点D、E分别在AB、AC上,∠ADE=∠C,如果AE=2,AB=3,△ADE的面积是4,则四边形BCED的面积是5. 如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.