题目内容
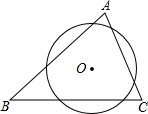 如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )
如图所示,在△ABC中,∠A=70°,⊙O截△ABC的三条边所得的弦长相等,则∠BOC的度数为( )| A、125° | B、130° |
| C、135° | D、160° |
考点:垂径定理,角平分线的性质
专题:
分析:连接OB,OC,先利用⊙O截△ABC的三条边所得的弦长相等,得出即O是△ABC的内心,从而,∠1=∠2,∠3=∠4,进一步求出∠BOC的度数.
解答:
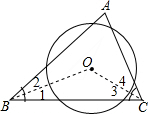 解:连接OB,OC.
解:连接OB,OC.
∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=
(180°-∠A)=
(180°-70°)=55°,
∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
故选A.
 解:连接OB,OC.
解:连接OB,OC.∵△ABC中∠A=70°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOC=180°-(∠1+∠3)=180°-55°=125°.
故选A.
点评:本题考查的是角平分线的性质,根据题意作出辅助线,构造三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
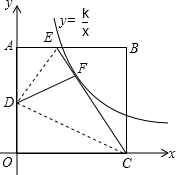 如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=
如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y= 如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是
如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是 如图,四边形ABCD中,AD=AB,∠ABC=∠ADC=90°,∠ACB=55°,则∠DAB的度数为
如图,四边形ABCD中,AD=AB,∠ABC=∠ADC=90°,∠ACB=55°,则∠DAB的度数为 已知数a、b、c在数轴上的位置如图所示,则|a-c|-|a+b+c|-|b-a|=
已知数a、b、c在数轴上的位置如图所示,则|a-c|-|a+b+c|-|b-a|=