题目内容
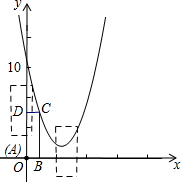 在直角坐标系中,抛物线y=x2+bx+c经过点(0,10)和点(4,2).
在直角坐标系中,抛物线y=x2+bx+c经过点(0,10)和点(4,2).(1)求这条抛物线的解析式.
(2)如图,在边长一定的矩形ABCD中,CD=1,点C在y轴右侧沿抛物线y=x2+bx+c滑动,在滑动过程中CD∥x轴,AB在CD的下方.当点D在y轴上时,AB落在x轴上.
①求边BC的长.
②当矩形ABCD在滑动过程中被x轴分成两部分的面积比为1:4时,求点C的坐标.
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求出二次函数解析式即可;
(2)①利用在y=x2-6x+10中,当x=1时,y=5,进而得出BC的长;
②利用当矩形ABCD在x轴上方部分的面积占这个矩形面积的
时,以及当矩形ABCD在x轴上方部分占这个矩形面积的
时,分别得出C点坐标即可.
(2)①利用在y=x2-6x+10中,当x=1时,y=5,进而得出BC的长;
②利用当矩形ABCD在x轴上方部分的面积占这个矩形面积的
| 1 |
| 5 |
| 4 |
| 5 |
解答:
解:(1)由已知,得
,
解得:
故这条抛物线的解析式为:y=x2-6x+10;
(2)①∵CD=1,点D在y 轴上,
∴点C的横坐标为1.
在y=x2-6x+10中,当x=1时,y=5.
∴边BC的长为5.
②∵矩形边长一定,∴BC=5.
当矩形ABCD在x轴上方部分的面积占这个矩形面积的
时,
∵BC=5,∴点C的纵坐标为1.
∴x2-6x+10=1,
即x2-6x+9=0,
∴C1(3,1).
当矩形ABCD在x轴上方部分占这个矩形面积的
时,
∵BC=5,∴点C的纵坐标为4.
∴x2-6x+10=4,
即x2-6x+6=0,
解得:x1=3+
,x2=3-
,
∴C2(3+
,4),C3(3-
,4).
|
解得:
|
故这条抛物线的解析式为:y=x2-6x+10;
(2)①∵CD=1,点D在y 轴上,
∴点C的横坐标为1.
在y=x2-6x+10中,当x=1时,y=5.
∴边BC的长为5.
②∵矩形边长一定,∴BC=5.
当矩形ABCD在x轴上方部分的面积占这个矩形面积的
| 1 |
| 5 |
∵BC=5,∴点C的纵坐标为1.
∴x2-6x+10=1,
即x2-6x+9=0,
∴C1(3,1).
当矩形ABCD在x轴上方部分占这个矩形面积的
| 4 |
| 5 |
∵BC=5,∴点C的纵坐标为4.
∴x2-6x+10=4,
即x2-6x+6=0,
解得:x1=3+
| 3 |
| 3 |
∴C2(3+
| 3 |
| 3 |
点评:此题主要考查了二次函数综合以及待定系数法求二次函数解析式以及一元二次方程的解法等知识,利用分类讨论得出是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
点(-2,-5)所在的象限是( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
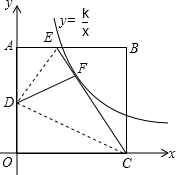 如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y=
如图,矩形ABCD的顶点O与直角坐标系的原点O重合,点A在y轴上,点C在x轴上,点E是AB边上一点,且BE=4,连接CE,把∠B沿CE对折,点B恰好落在线段AO上的点D处,把∠A沿DE对折,点A与CE线段上的点F重合,则过点F的反比例函数y= 如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是
如图,某水库大坝横截面示意图,其中AB,CD分别表示水库上下底面的水平线,∠ABC=120°,BC的长是50米,则水库大坝的高度h是 如图,四边形ABCD中,AD=AB,∠ABC=∠ADC=90°,∠ACB=55°,则∠DAB的度数为
如图,四边形ABCD中,AD=AB,∠ABC=∠ADC=90°,∠ACB=55°,则∠DAB的度数为