题目内容
计算: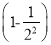 
×
×
×…×
×
.
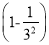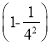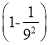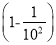【解析】试题分析：先把所给式子的每一个括号内的式子利用平方差公式因式分解，分别计算后约分即可.
试题解析：
原式=××××1+××…××
=××××××…××
=.
练习册系列答案
状元坊全程突破导练测系列答案
相关题目
如图，在直角坐标系内，O为原点，点A的坐标为(10，0)，点B在第一象限内，BO＝5，sin∠BOA＝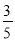
. 求：(1)点B的坐标；(2)cos∠BAO的值．
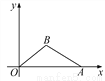
（1）点B的坐标为(4，3)；（2）cos∠BAO＝.
【解析】试题分析：（1）作BH⊥OA， 垂足为H，在Rt△OHB中，根据锐角三角函数的定义及已知条件求得BH的长，再根据勾股定理求得OH的长，即可得点B的坐标；（2）先求得AH的长，在Rt△AHB中，根据勾股定理求得AB的长，根据锐角三角函数的定义即可求得cos∠BAO的值．
试题解析：
(1)如图所示，作BH⊥OA， 垂足... 两平行直线被第三条直线所截，同位角的平分线（ ）
A. 互相重合 B. 互相平行
C. 互相垂直 D. 相交
B
【解析】如图，AB∥CD，HI与AB，CD分别交于点M、N，EM，FN分别是∠AMH，∠CNH的平分线，由AB∥CD，根据平行线的性质可得∠AMH=∠CNH，又因EM，FN分别是∠AMH，∠CNH的平分线，所以∠1= ∠AMH，∠2=∠CNH，根据等量代换可得∠1=∠2，根据同位角相等，两直线平行即可得EM∥FN，故选B. 设直线l1和直线l2平行，且l1和l2间的距离为a．如果线段AB在l1的右侧，并设AB关于l1的对称图形是A′B′，而A′B′关于l2的对称图形是A″B″（如图），那么，线段AB和A″B″有什么关系？
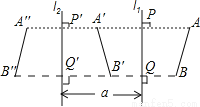
A''B''平行且等于AB，理由见解析
【解析】试题分析：根据轴对称的性质，及在平面内垂直于同一条直线的两条直线互相平行，即可判断ABB''A''为平行四边形，继而得出答案．
试题解析：【解析】
因为l1平行于l2，并且AA″垂直于l1，当然也垂直于l2，同理BB″也垂直于l1和l2．
又在平面内垂直于同一条直线的两条直线互相平行，
所以AA″∥BB″①
另一方面，... 如图，△ABC和△A′B′C′关于直线l对称，下列结论中：
①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；
③l垂直平分CC′；
④直线BC和B′C′的交点不一定在l上，
正确的有（ ）
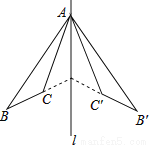
A. 4个 B. 3个 C. 2个 D. 1个
B
【解析】【解析】
∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故... 先化简,再求值:-(a2-2ab)·9a2-(9ab3+12a4b2)÷3ab,其中a=-1,b=2.
-49
【解析】试题分析：利用单项式乘以单项式的乘法法则和多项式除以单项式的除法法则计算后，合并同类项化为最简，再代入求值即可.
试题解析：
原式=-9a4+18a3b-3b2-4a3b=-9a4+14a3b-3b2.
将a=-1,b=2代入得,原式=-49. 计算:(-2)2 016+(-2)2 017=___________.
-22 016
【解析】 (-2)2 016+(-2)2 017=(-2)2 016(1-2)=-22 016. 下列图形是轴对称图形吗？如果是轴对称图形，请画出它的对称轴.
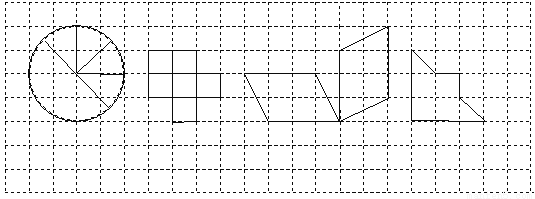
见解析
【解析】试题分析：根据轴对称图形的性质判断出轴对称图形，进而画出对称轴得出即可．
试题解析：第一、二、四中图形是轴对称图形，如图所示： 已知函数y=
x3+2，不画图象，解答下列问题：
（1）判断A（0，2）、B（2，0）、C（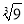
， ﹣1）三点是否在该函数图象上，说明理由；
（2）若点P（a，0）、Q（﹣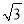
， b）都在该函数的图象上，试求a、b的值．
(1) B，C点不在该函数图象上，A点在该函数图象上；(2) a=,b=
【解析】试题分析：（1）分别将A，B，C点代入函数关系式进而判断即可；（2）分别将P，Q点代入函数关系式进而得出答案．
试题解析：
（1）当x=0时，y=2，
当x=2时，y=+2=，
当x=时，y=5，
故B，C点不在该函数图象上，A点在该函数图象上；
（2）当y=0时，0=x3+...