题目内容

如图，在?ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC等于（　　）
A、3：2B、3：1
C、1：2D、1：1
考点：相似三角形的判定与性质,平行四边形的性质
专题：
分析：根据题意得出△DEF∽△BCF，进而得出
DE
BC
=
EF
FC
，利用点E是边AD的中点得出答案即可．
解答：解：∵四边形ABCD为平行四边形，
∴AD∥BC，
∴△DEF∽△BCF，
∴
DE
BC
=
EF
FC
，
∵点E是边AD的中点，
∴AE=DE=
1
2
AD，
∴
EF
FC
=
1
2
．
故选：C．
点评：此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识，得出△DEF∽△BCF是解题关键．
练习册系列答案
相关题目
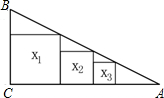如图，在Rt△ABC中，∠C=90°，BC=1，AC=2，把边长分别为x1，x2，x3…，xn的n个正方形依次放入△ABC中，请回答下列问题：
（1）按要求填表
n123
xn
 
 
 
（2）第n个正方形的边长xn=
 
；
（3）有甲、乙两同学，甲从2，4，6，8这四个数字中抽取2个，乙得到剩下的两个数字，甲同学抽取的数字表示m，n，乙同学抽取的数字表示p，q，求甲乙同学抽取的数字恰好能符合关系式xm•xn=xp•xq的概率．
在一个边长为a（单位：cm）的正方形ABCD中．
（1）如图1，如果N是AD中点，F为AB中点，连接DF，CN．
①求证：DF=CN；
②连接AC．则DH：HE：EF=
 
．（直接写出结果）
（2）如图2，如果点E、M分别是线段AC、CD上的动点，假设点E从点A出发，以
2
cm/s速度沿AC向点C运动，同时点M从点C出发，以1cm/s的速度沿CD向点D运动，运动时间为t（t＞0），连结DE并延长，交正方形的边于点F，过点M作MN⊥DF于H，交AD于N．求证：当点F是边AB中点时，DM=2CM．
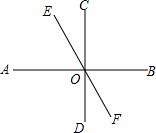如图，已知直线AB，CD，EF相交于点O，CD⊥AB，∠DOF：∠AOD=1：3，求∠COE和∠AOE的度数．
下列图形中，对称轴最多的是（　　）
A、等腰三角形
B、等边三角形
C、直角三角形
D、等腰直角三角形
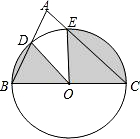如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=72°，BC=4．求图中阴影部分的总周长和总面积（结果保留π）
如果n边形的内角和等于外角和的3倍，那么n的值是（　　）
A、5B、6C、7D、8
用“＜”、“＞”或“=”填空：
3
2
3
 
12
．
如图，点E，F分别是矩形ABCD的边AD，BC的三等分点（距D、C近），若矩形ABFE与矩形ABCD相似，则矩形ABCD的AD：AB是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网