题目内容
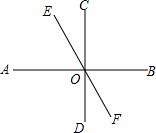 如图,已知直线AB,CD,EF相交于点O,CD⊥AB,∠DOF:∠AOD=1:3,求∠COE和∠AOE的度数.
如图,已知直线AB,CD,EF相交于点O,CD⊥AB,∠DOF:∠AOD=1:3,求∠COE和∠AOE的度数.考点:对顶角、邻补角
专题:
分析:要求∠COE的度数,根据对顶角相等,只需求出∠DOF的度数,由CD⊥AB,可得∠AOD=90°,然后根据∠DOF:∠AOD=1:3,可求∠DOF的度数,即可求∠COE的度数;而∠AOE与∠COE互余,所以∠AOE的度数可求.
解答:解:∵CD⊥AB,
∴∠AOD=∠AOC=90°,
∵∠DOF:∠AOD=1:3,
∴∠DOF=
∠AOD=
×90°=30°,
∴∠EOC=∠DOF=30°,
∵∠EOC+∠AOE=∠AOC=90°,
∴∠AOE=90°-30°=60°.
答:∠COE和∠AOE的度数分别为:30°、60°.
∴∠AOD=∠AOC=90°,
∵∠DOF:∠AOD=1:3,
∴∠DOF=
| 1 |
| 3 |
| 1 |
| 3 |
∴∠EOC=∠DOF=30°,
∵∠EOC+∠AOE=∠AOC=90°,
∴∠AOE=90°-30°=60°.
答:∠COE和∠AOE的度数分别为:30°、60°.
点评:本题考查了对顶角、邻补角.解题的关键是:充分利用已知条件和隐含条件(平角、余角、补角、对顶角等).

练习册系列答案
相关题目
 如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在?ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、3:1 |
| C、1:2 | D、1:1 |

 如图,三条直线AB,CD,EF相交于点O,∠1=65°,∠2=52°,求∠COE的度数.
如图,三条直线AB,CD,EF相交于点O,∠1=65°,∠2=52°,求∠COE的度数.
 如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.
如图所示,直线AB,CD交于点O,OE平分∠DOB,且∠AOD:∠DOE=3:1,求∠AOC的度数.