题目内容
19.阅读下面问题:$\frac{1}{1+\sqrt{2}}$=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)(\sqrt{2}-1)}$=$\sqrt{2}$-1;
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}$=$\sqrt{3}$-$\sqrt{2}$;
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{(\sqrt{5}+2)(\sqrt{5}-2)}$=$\sqrt{5}$-2.
试求:
(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)的值.
(2)利用上面所揭示的规律计算:$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$.
分析 (1)根据平方差公式,可分母有理化;
(2)根据分母有理化,可出现互为相反数的项,根据合并同类二次根式,可得答案.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+$\sqrt{5}$-$\sqrt{4}$+…+$\sqrt{2015}$-$\sqrt{2014}$+$\sqrt{2016}$-$\sqrt{2015}$
=$\sqrt{2016}$-1
=12$\sqrt{14}$-1.
点评 主要考查二次根式的有理化.根据二次根式的乘除法法则进行二次根式有理化.二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.

练习册系列答案
相关题目
4.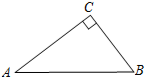 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( )
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
11.若2x=3y,则$\frac{2x+y}{x-3y}$的值是( )
| A. | -1 | B. | $-\frac{8}{3}$ | C. | 1 | D. | $\frac{8}{3}$ |
1. 如图所示的几何体,其主视图是( )
如图所示的几何体,其主视图是( )
 如图所示的几何体,其主视图是( )
如图所示的几何体,其主视图是( )| A. |  | B. |  | C. |  | D. |  |
 下面的框图表示了解这个方程的流程:其中,“移项”这一步骤的依据是等式的性质1.
下面的框图表示了解这个方程的流程:其中,“移项”这一步骤的依据是等式的性质1. 如图,每个正方形的边长为a.
如图,每个正方形的边长为a. 小明家住房的结构如图所示(图形均为长方形,单位:米),小明爸爸打算把卧室以外的部分都铺上地板砖,请问
小明家住房的结构如图所示(图形均为长方形,单位:米),小明爸爸打算把卧室以外的部分都铺上地板砖,请问