若2x=3y.则$\frac{2x+y}{x-3y}$的值是( )A．-1B．$-\frac{8}{3}$C．1D．$\frac{8}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

11．若2x=3y，则$\frac{2x+y}{x-3y}$的值是（　　）

A．

-1

B．

$-\frac{8}{3}$

C．

D．

$\frac{8}{3}$

分析利用已知得出x与y的关系，进而代入原式求出答案．

解答解：∵2x=3y，
∴x=$\frac{3}{2}$y，
∴$\frac{2x+y}{x-3y}$=$\frac{3y+y}{\frac{3}{2}y-3y}$=$\frac{4y}{-\frac{3}{2}y}$=-$\frac{8}{3}$．
故选：B．

点评此题主要考查了分式的值，正确得出x与y之间的关系是解题关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

相关题目

（x²）³=x⁵

a³•a⁴=a¹²

2．小毅和小明同时从学校出发到科技馆参加活动，小毅每小时走6千米，小明每小时走8千米，走了1小时后，小明忘带材料返回学校取材料，立即按原路去追小毅．小明几小时追上小毅？

19．阅读下面问题：
$\frac{1}{1+\sqrt{2}}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1；
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$；
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{（\sqrt{5}+2）（\sqrt{5}-2）}$=$\sqrt{5}$-2．
试求：
（1）$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n为正整数）的值．
（2）利用上面所揭示的规律计算：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$．

6．计算：$\sqrt{4}$-（π-3）⁰-（$\frac{1}{2}$）^-1+|-3|．

16．把2ab²-4ba+2a分解因式的结果是（　　）

3．化简$\sqrt{18}$的结果是（　　）

20．已知抛物线y=x²-4x+3，求这条抛物线与x轴交点的坐标以及当y＞0时，x的取值范围．

13．

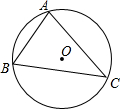如图，⊙O是△ABC的外接圆，弦AC的长为3，sinB=$\frac{3}{4}$，则⊙O的半径为（　　）

试题分类