题目内容

4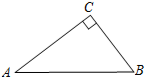．如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，则sinB的值等于（　　）
A．$\frac{4}{3}$B．$\frac{3}{4}$C．$\frac{4}{5}$D．$\frac{3}{5}$

分析 根据勾股定理，可得AB的长，根据在直角三角形中，锐角的正弦为对边比斜边，可得答案．

解答 解：在Rt△ABC中，由勾股定理，得
AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5．
sinB=$\frac{AC}{AB}$=$\frac{4}{5}$，
故选：C．

点评 本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．

练习册系列答案
相关题目
14．解方程：$1+\frac{x-1}{2}=\frac{x+2}{6}$．
15．二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列说法：①abc＜0；②2a+b=0；③9a+3b+c＞0；④当-1＜x＜3时，y＜0；⑤当x＜0时，y随x的增大而减小，其中正确的个数为（　　）
A．1B．2C．3D．4
12．若点P（1，a）与Q（b，2）关于x轴对称，则代数式（a+b）2015的值为（　　）
A．-1B．1C．-2D．2
19．阅读下面问题：
$\frac{1}{1+\sqrt{2}}$=$\frac{1×（\sqrt{2}-1）}{（\sqrt{2}+1）（\sqrt{2}-1）}$=$\sqrt{2}$-1；
$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\frac{\sqrt{3}-\sqrt{2}}{（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）}$=$\sqrt{3}$-$\sqrt{2}$；
$\frac{1}{\sqrt{5}+2}$=$\frac{\sqrt{5}-2}{（\sqrt{5}+2）（\sqrt{5}-2）}$=$\sqrt{5}$-2．
试求：
（1）$\frac{1}{\sqrt{n+1}+\sqrt{n}}$（n为正整数）的值．
（2）利用上面所揭示的规律计算：$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$+$\frac{1}{\sqrt{2015}+\sqrt{2016}}$．
9．在$\frac{1}{x}，\frac{3}{x+y}，\frac{1}{2}，\frac{2xy}{π}，-\frac{x+1}{3}$中，分式有（　　）
A．1个B．2个C．3个D．4个
16．把2ab2-4ba+2a分解因式的结果是（　　）
A．2ab（b-2）+2aB．2a（b2-2b）C．2a（b+1）（b-1）D．2a（b-1）2
13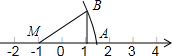．如图，Rt△MBC中，∠MCB=90°，点M在数轴-1处，点C在数轴1处，MA=MB，BC=1，则数轴上点A对应的数是（　　）
A．$\sqrt{5}$+1B．-$\sqrt{5}$+1C．-$\sqrt{5}$-lD．$\sqrt{5}$-1
6．如图，AB是⊙O的直径，AC是弦，半径OD⊥AC于点E，过点D的切线与BA延长线交于点F．
（1）求证：∠CDB=∠BFD；
（2）若AB=10，AC=8，求DF的长．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网