题目内容
7.一个不透明的盒子中装有10个黑球和若干个白球,它们除颜色不同外,其余均相同,从盒子中随机摸出一球记下其颜色,再把它放回盒子中摇匀,重复上述过程,共试验400次,其中有240次摸到白球,由此估计盒子中的白球大约有15个.分析 在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,设未知数列出方程求解.
解答 解:∵共试验400次,其中有240次摸到白球,
∴白球所占的比例为$\frac{240}{400}$=0.6,
设盒子中共有白球x个,则$\frac{x}{x+10}$=0.6,
解得:x=15,
故答案为:15.
点评 本题考查利用频率估计概率.大量反复试验下频率稳定值即概率.关键是根据白球的频率得到相应的等量关系.

练习册系列答案
相关题目
15. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法:①abc<0;②2a+b=0;③9a+3b+c>0;④当-1<x<3时,y<0;⑤当x<0时,y随x的增大而减小,其中正确的个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
12.若点P(1,a)与Q(b,2)关于x轴对称,则代数式(a+b)2015的值为( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
16.把2ab2-4ba+2a分解因式的结果是( )
| A. | 2ab(b-2)+2a | B. | 2a(b2-2b) | C. | 2a(b+1)(b-1) | D. | 2a(b-1)2 |
9. 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
 如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
如图,AB、CD、EF、MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
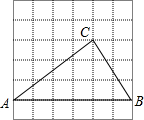 如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosA=$\frac{4}{5}$.
如图,网格中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosA=$\frac{4}{5}$.