题目内容
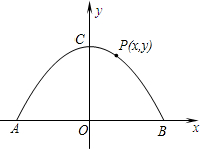 如图,二次函数y=-
如图,二次函数y=-| 1 |
| 2 |
(1)直接写出A、B、C点的坐标;
(2)设点P(x,y)为该图象上的任意一点,连接OP,求OP长度的范围.
考点:二次函数的性质,二次函数的最值
专题:
分析:(1)根据函数解析式写出A、B、C点的坐标;
(2)依据勾股定理以及抛物线的解析式即可求得.
(2)依据勾股定理以及抛物线的解析式即可求得.
解答:解:(1)A(-2,0),B(2,0),C(0,2).
(2)由题意得,OP2=x2+y2=x2+(-
x2+2)2=
(x2-2)2+3(-2≤x≤2);
当x2=2时,即x=±
时,OP2取得最小值,最小值为3.即OP的最小值为
.
当x=-2、0或2时,OP2取得最大值,最大值为4.即OP的最大值为2,
所以OP长度的范围为:
≤OP≤2.
(2)由题意得,OP2=x2+y2=x2+(-
| 1 |
| 2 |
| 1 |
| 4 |
当x2=2时,即x=±
| 2 |
| 3 |
当x=-2、0或2时,OP2取得最大值,最大值为4.即OP的最大值为2,
所以OP长度的范围为:
| 3 |
点评:本题考查了二次函数的性质,勾股定理的应用.

练习册系列答案
相关题目
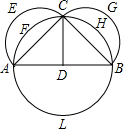 如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:
如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:
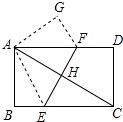 如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.