题目内容
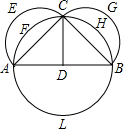 如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:
如图,分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆.则:①S半圆AECA+S半圆BGCB=S半圆ALBA;
②S月形AECF=2S弓形AFCA;
③S弓形AFCA+S弓形CHBC=
| 1 |
| 2 |
④S月形AECF+S月形BGCH=S△ABC.
正确的结论有( )
| A、①②③ | B、①④ |
| C、②③④ | D、①②③④ |
考点:勾股定理
专题:
分析:根据等腰直角三角形的性质以及圆的面积公式,分别表示出各部分面积进而判断得出即可.
解答:解:∵分别以等腰Rt△ABC的边AC、BC为直径画半圆,以边AB为直径画圆,
∴∠ACB=∠ADC=90°,∠CAB=∠CBA=45°,
设AC=2x,则BC=2x,AB=2
x,
①∵S半圆AECA=
πx2,S半圆BGCB=
πx2,S半圆ALBA=
π(
x)2=πx2,
∴S半圆AECA+S半圆BGCB=S半圆ALBA,故此选项正确;
②∵S弓形AFCA=S扇形ADC-S△ADC=
πx2-
×
x×
x=
x2(π-2),
S月形AECF=
πx2-
x2(π-2)=x2,
∴S月形AECF≠2S弓形AFCA,故此选项错误;
③∵S弓形AFCA=S弓形CHBC=
x2(π-2),
∴S弓形AFCA+S弓形CHBC=(π-2)x2,
S△ABC=
×2x×2x=2x2,
∴S弓形AFCA+S弓形CHBC≠
S△ABC,故此选项错误;
④∵S月形AECF=S月形BGCH=x2,
∴S月形AECF+S月形BGCH=2x2,S△ABC=
×2x×2x=2x2,
∴S月形AECF+S月形BGCH=S△ABC,故此选项正确.
故选:B.

∴∠ACB=∠ADC=90°,∠CAB=∠CBA=45°,
设AC=2x,则BC=2x,AB=2
| 2 |
①∵S半圆AECA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
∴S半圆AECA+S半圆BGCB=S半圆ALBA,故此选项正确;
②∵S弓形AFCA=S扇形ADC-S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
S月形AECF=
| 1 |
| 2 |
| 1 |
| 2 |
∴S月形AECF≠2S弓形AFCA,故此选项错误;
③∵S弓形AFCA=S弓形CHBC=
| 1 |
| 2 |
∴S弓形AFCA+S弓形CHBC=(π-2)x2,
S△ABC=
| 1 |
| 2 |
∴S弓形AFCA+S弓形CHBC≠
| 1 |
| 2 |
④∵S月形AECF=S月形BGCH=x2,
∴S月形AECF+S月形BGCH=2x2,S△ABC=
| 1 |
| 2 |
∴S月形AECF+S月形BGCH=S△ABC,故此选项正确.
故选:B.
点评:此题主要考查了勾股定理以及圆面积公式和三角形面积求法,根据题意求出特殊图形面积进而得出一般图形面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点P在第二象限,且到x轴的距离为2,到y轴的距离为3.点P坐标是( )
| A、(-2,3) |
| B、(-2,3) |
| C、(-3,2) |
| D、(3,-2) |
1克大米约50粒,如果每人每天浪费1粒大米,那么全国13亿人每天就要浪费大米约( )
| A、26千克 |
| B、2.6×102千克 |
| C、2.6×103千克 |
| D、2.6×104千克 |
 如图,直线y=x+b交x轴于点A(-2,0),则不等式x+b<0解集是( )
如图,直线y=x+b交x轴于点A(-2,0),则不等式x+b<0解集是( )| A、x<-2 | B、x<2 |
| C、x>-2 | D、x>2 |
如果两个角的两边分别垂直,那么这两个角( )
| A、都等于90° | B、相等 |
| C、相等或互余 | D、相等或互补 |
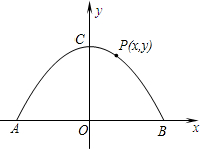 如图,二次函数y=-
如图,二次函数y=-